Notes
two rectangles overlapping a square solution
Solution to the Two Rectangles Overlapping a Square Puzzle
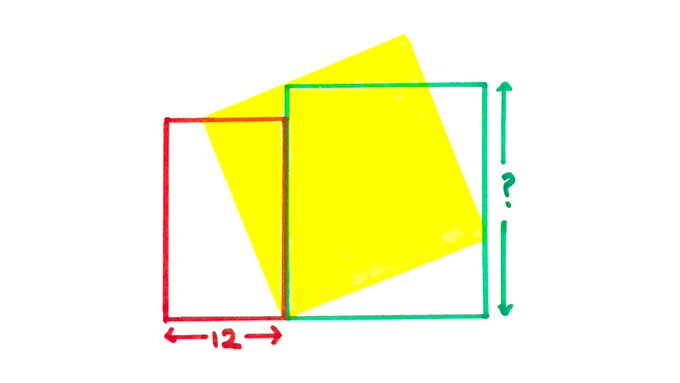
The yellow square has double the area of the red rectangle. How tall is the green rectangle?
Solution by Dissection and Area of a Rectangle
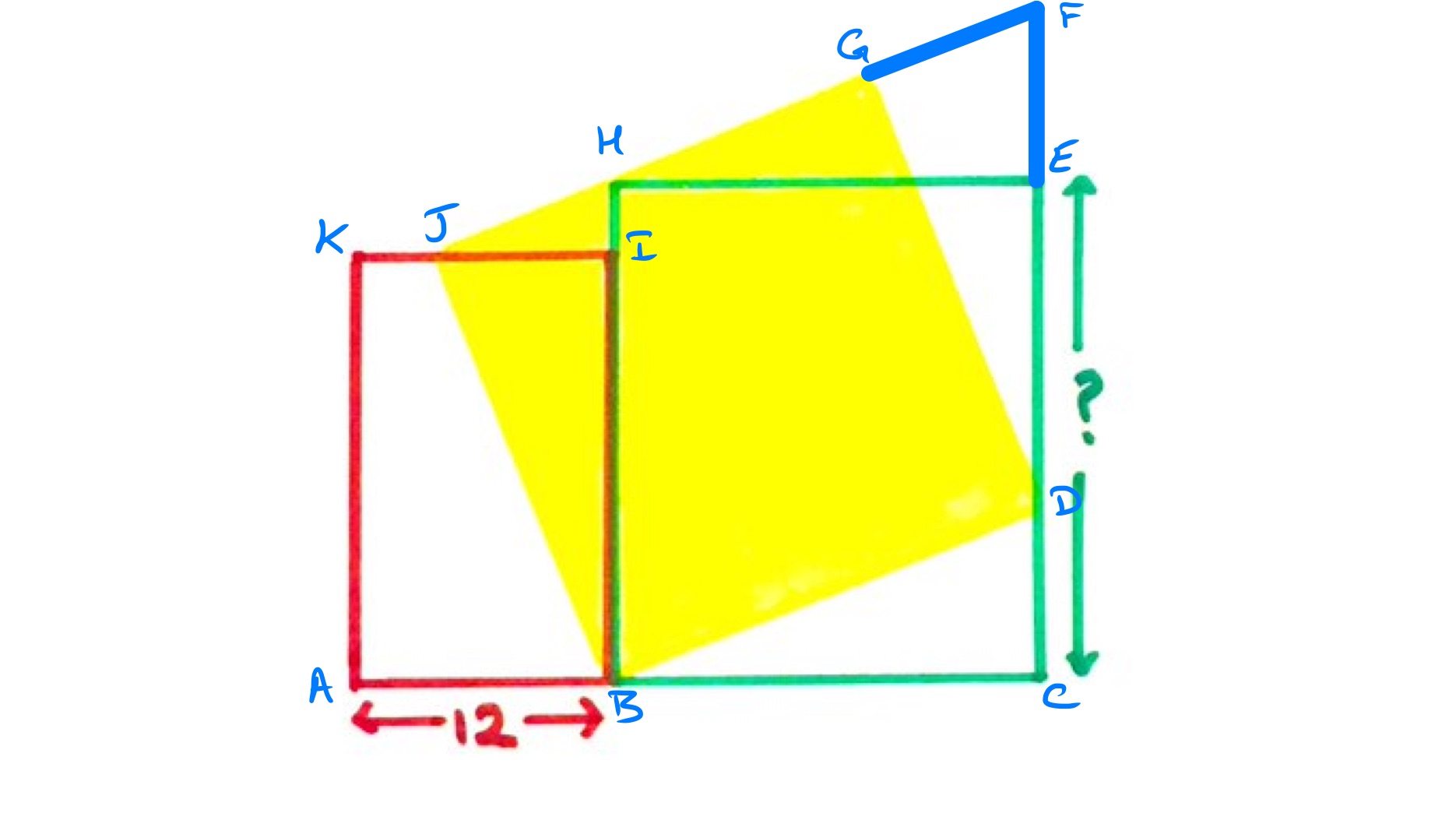
Triangle is congruent to triangle , then triangle is congruent to triangle . These establish that the green rectangle has the same area as the yellow square. (This can also be established by shears: first, parallel to ; second, parallel to .)
Triangle is congruent to triangle , meaning that the length of is the length of . Therefore, since the green rectangle has twice the area of the red, the length of must be twice that of , namely .