Notes
two rectangles of equal area solution
Solution to the Two Rectangles of Equal Area Puzzle
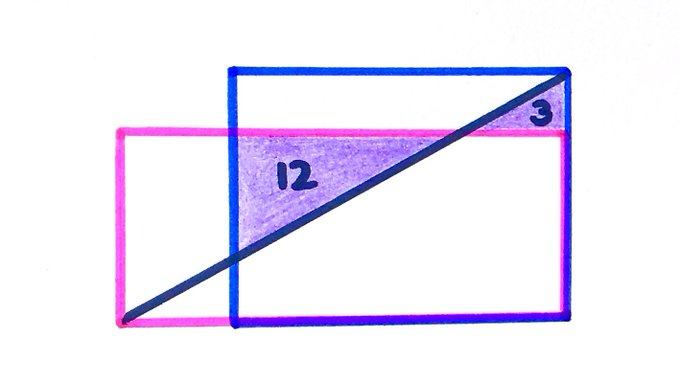
The pink and blue rectangles have the same area. What is it?
Solution by Similarity and Vertically Opposite Angles
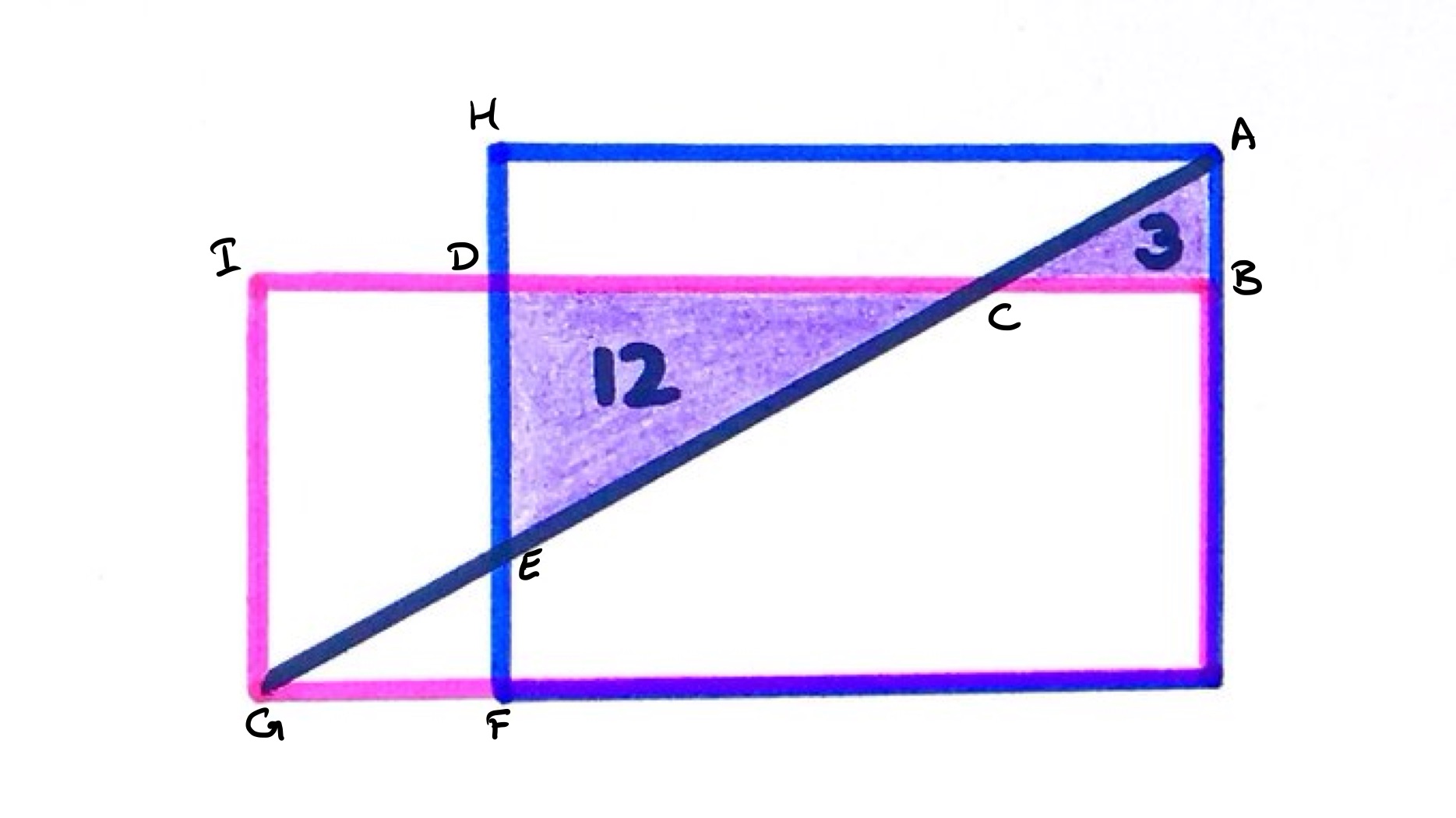
With the points labelled as above, let have length and have length . The area of triangle is so .
The triangles and are similar since they are both right-angled and angles and are equal as they are vertically opposite. The area scale factor is , so the length scale factor is . This means that the length of is twice that of , and of is twice that of . In terms of and , has length and has length .
Triangle is also right-angled and angles and are equal as they are vertically opposite. So is similar to . Let the scale factor be , so that the length of is and of is .
Rectangle has width and height while rectangle has width and height . As the pink and blue rectangles have the same area, these two rectangles also have the same area. So:
which simplifies to . The solution to this is (the other possible solution is but is a positive scale factor). So is actually congruent to and the length of is . The area of the blue rectangle is therefore .