Notes
two rectangles in a semi-circle solution
Two Rectangles in a Semi-Circle
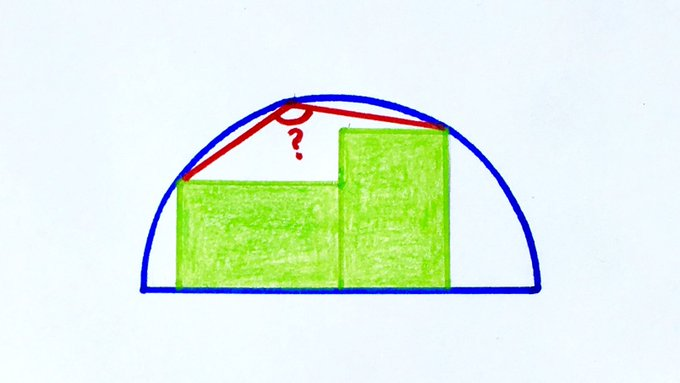
Two congruent rectangles sitting in a semicircle. What’s the angle?
Solution by Properties of Chords and Angle at the Circumference is Half the Angle at the Centre
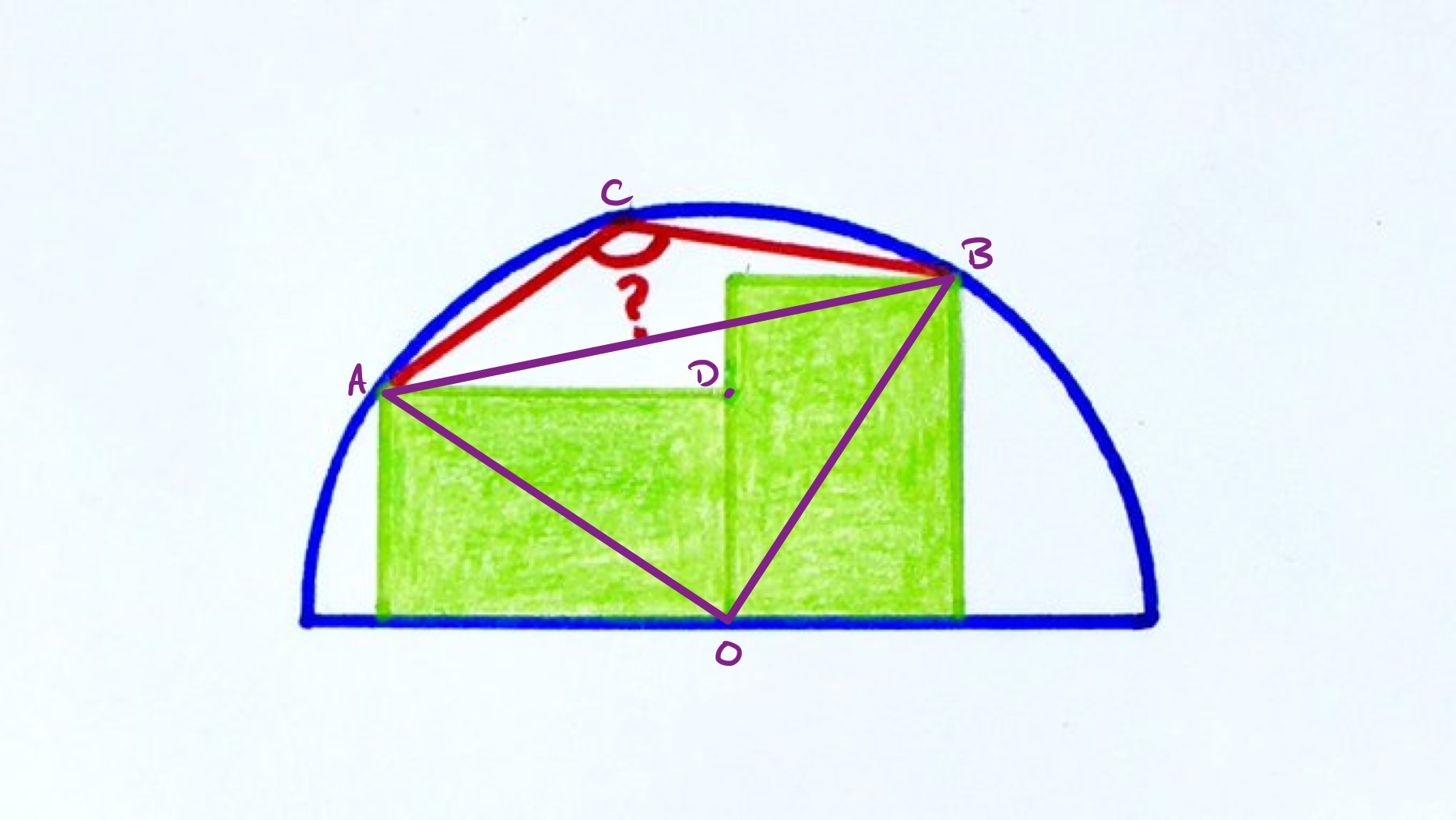
As the rectangles are congruent, the diagonals and are of equal length and so triangle is isosceles. This means that point lies on the perpendicular bisector of . Since is a chord, the centre of the circle also lies on that perpendicular bisector. Since is also on the diameter, then, it is the centre.
Using the fact that the angle at the circumference is half the angle at the centre, angle is half of angle , read anti-clockwise from to . As the rectangles are congruent, angles and add up to , so angle is , and hence angle is .