Notes
two rectangles and a square solution

Solution to the Two Rectangles and a Square Puzzle

Solution by Congruent Shapes and Similar Triangles

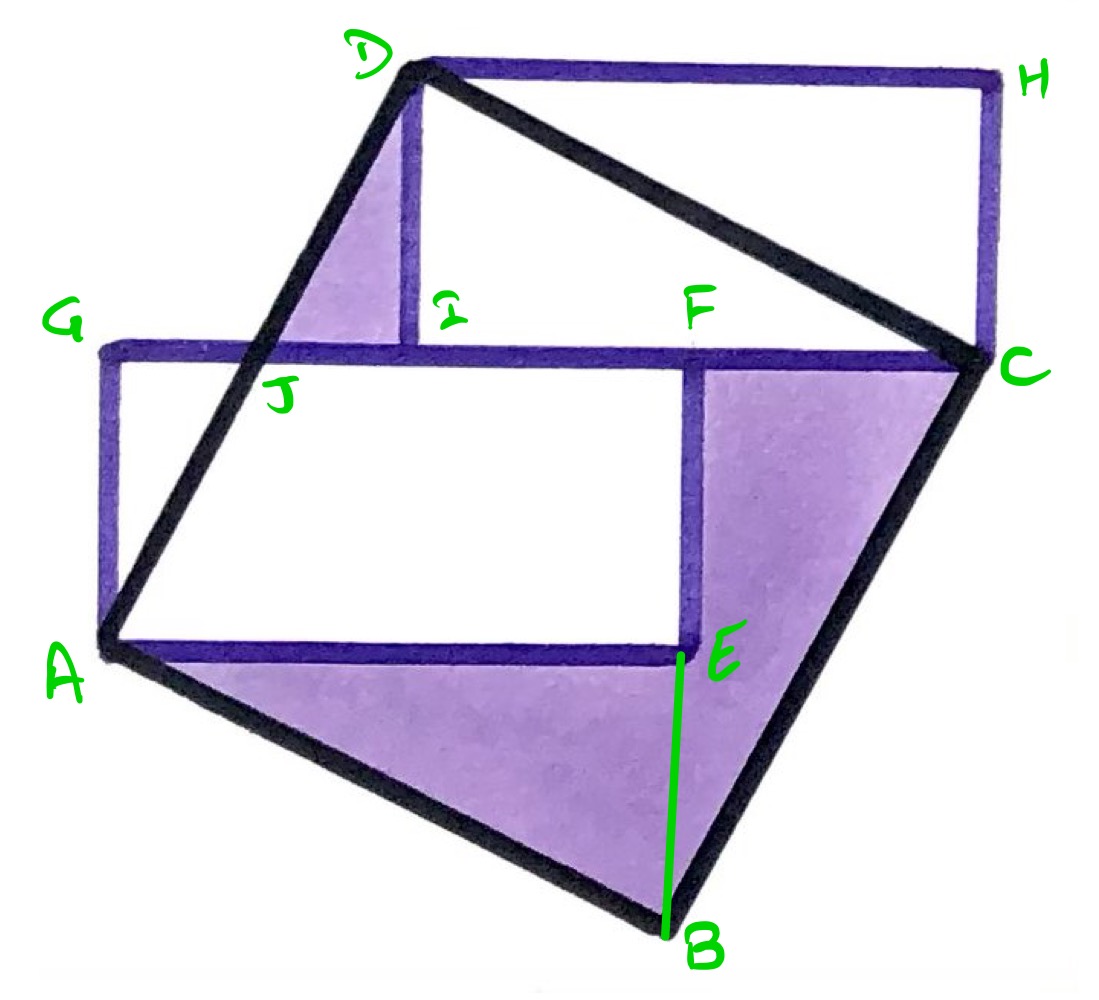
Label the points as above.

There are several congruent triangles. Triangles $D H C$ and $A E B$ are congruent, since $D C$ and $A B$ are opposite sides of the same square, and $D H$ and $A E$ are parallel sides of congruent rectangles. This establishes that $F E B$ is a straight line. In triangle $B F C$, angle $B \hat{F} C$ is a right-angle, then angle $C \hat{B} F$ and angle $E \hat{B} A$ add up to $90^\circ$, but then so also angles $E \hat{B} A$ and $B \hat{A} E$ also add up to $90^\circ$, so angles $C \hat{B} F$ and $B \hat{A} E$ are equal. Therefore triangles $B F C$ and $A E B$ are similar, but also $A B$ and $B C$ are the same length so they are in fact congruent.

This establishes $F B$ as having the same length as $A E$, but also the length of $F B$ is twice that of $F E$, so the sides of the rectangles are in the ratio $2 : 1$.

Triangles $D I J$ and $A G J$ are also both right-angled, and angles $D \hat{J} I$ and $G \hat{J} A$ are equal as they are vertically opposite. Since $D I$ and $A G$ are the same length, triangles $D I J$ and $A G J$ are therefore congruent. This means that the total area of the square is two and a half rectangles: match triangles $D I J$ with $A G J$ and $A E B$ with $D H C$, leaving just the half rectangle $B F C$ unaccounted for.

The shaded region accounts for one and an eighth of a rectangle: triangles $B F C$ and $A E B$ comprise one rectangle, while $D I J$ is similar to $B F C$ but with length scale factor $\frac{1}{2}$ so area scale factor $\frac{1}{4}$.

Hence the fraction that is shaded is: