Notes
two rectangles and a semi-circle solution
Solution to the Two Rectangles and a Semi-Circle Puzzle
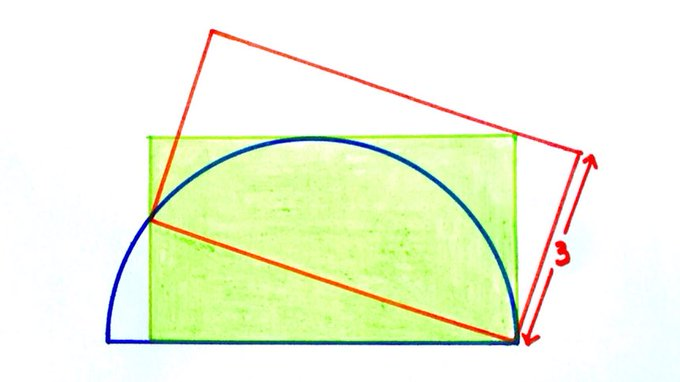
Two rectangles and a semicircle. What’s the shaded area?
Solution by Dissection, Angle in a Semi-Circle, and Similar Triangles
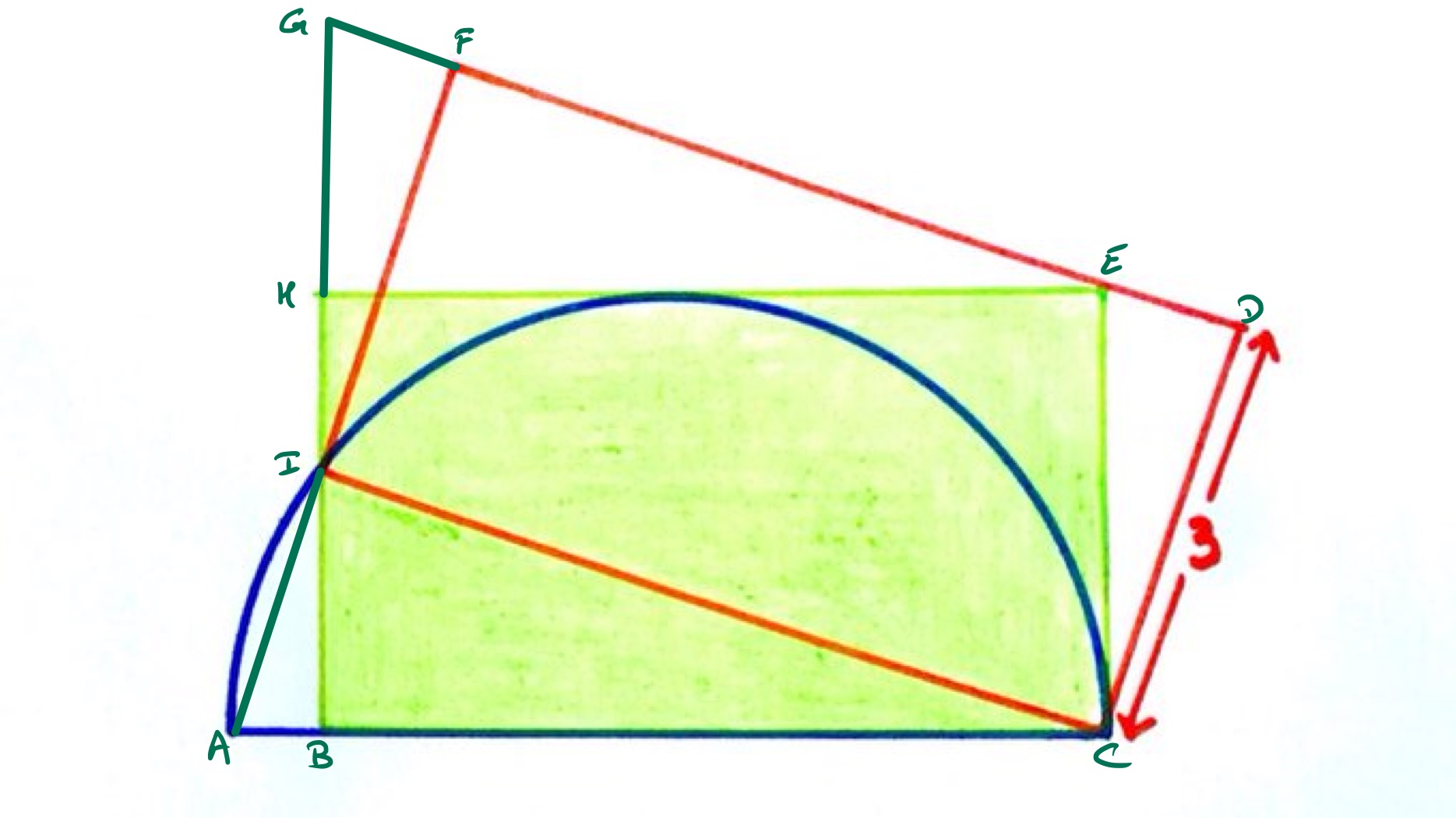
With the points labelled as above, first note that there is a dissection argument to show that the two rectangles have the same area. Triangles and are congruent, so the green rectangle has the same area as parallelogram . Then triangles and are also congruent, so the parallelogram has the same area as the red rectangle.
Alternatively, this can be seen by a composition of two shears centred at . The first is vertical and takes to . The second is parallel to and takes to .
Triangle is right-angled since the angle in a semi-circle is . It is similar to triangle since each of angles and makes a right-angle when added to angle . Since is a radius of the semi-circle and a diameter, the length scale factor is . Therefore the length of is twice that of , so is of length . The area of the red rectangle, and hence also of the green, is then .
Solution by Invariance Principle
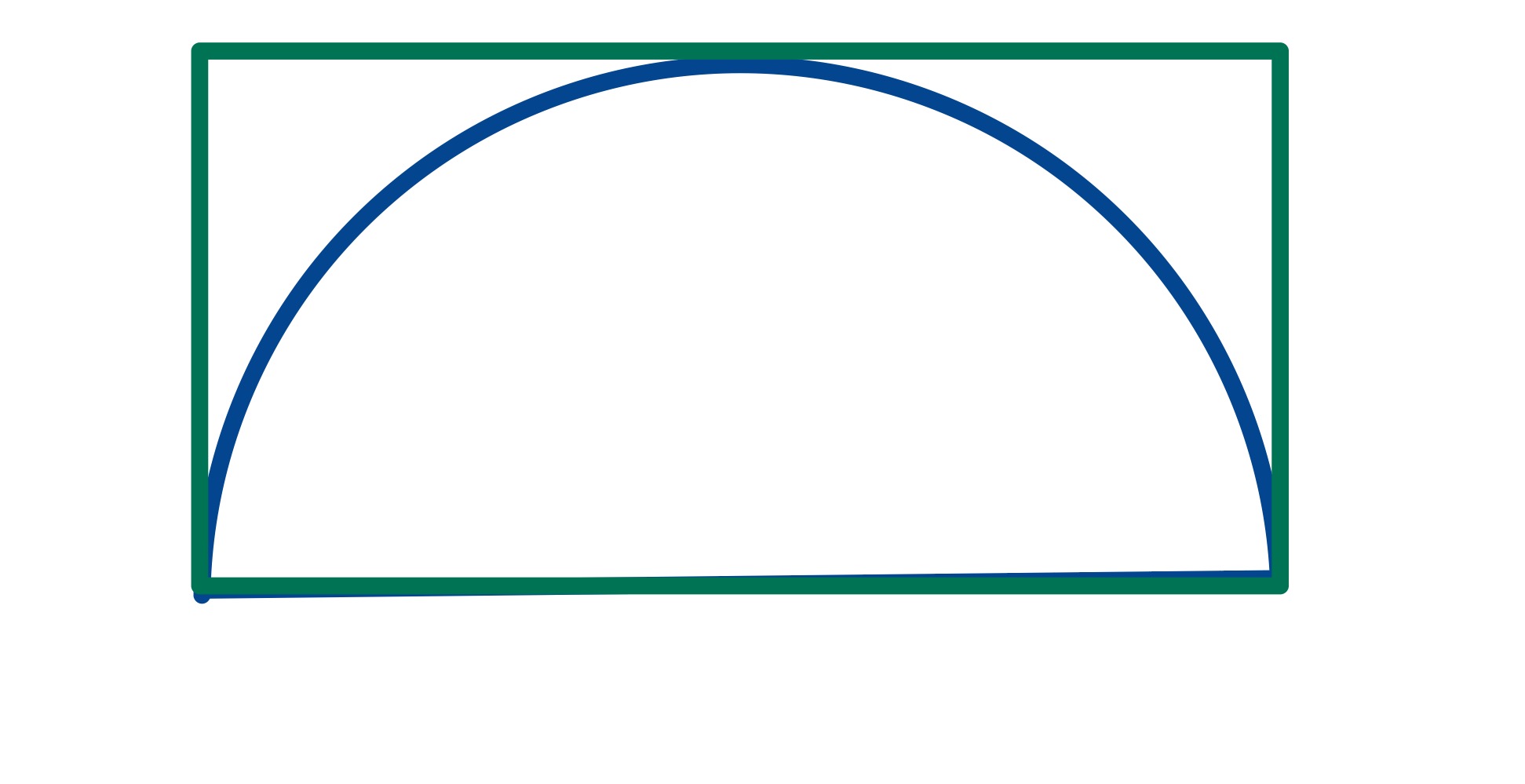
In this special case, the red rectangle coincides with the green and so they have the same area. Also, the height of the red rectangle is the radius of the semi-circle, so its diameter is . The area of the rectangle is therefore .