Notes
two quarter circles solution

Solution to the Two Quarter Circles Puzzle

Solution by Angle at the Circumference is Half the Angle at the Centre and Angles in the Same Segment

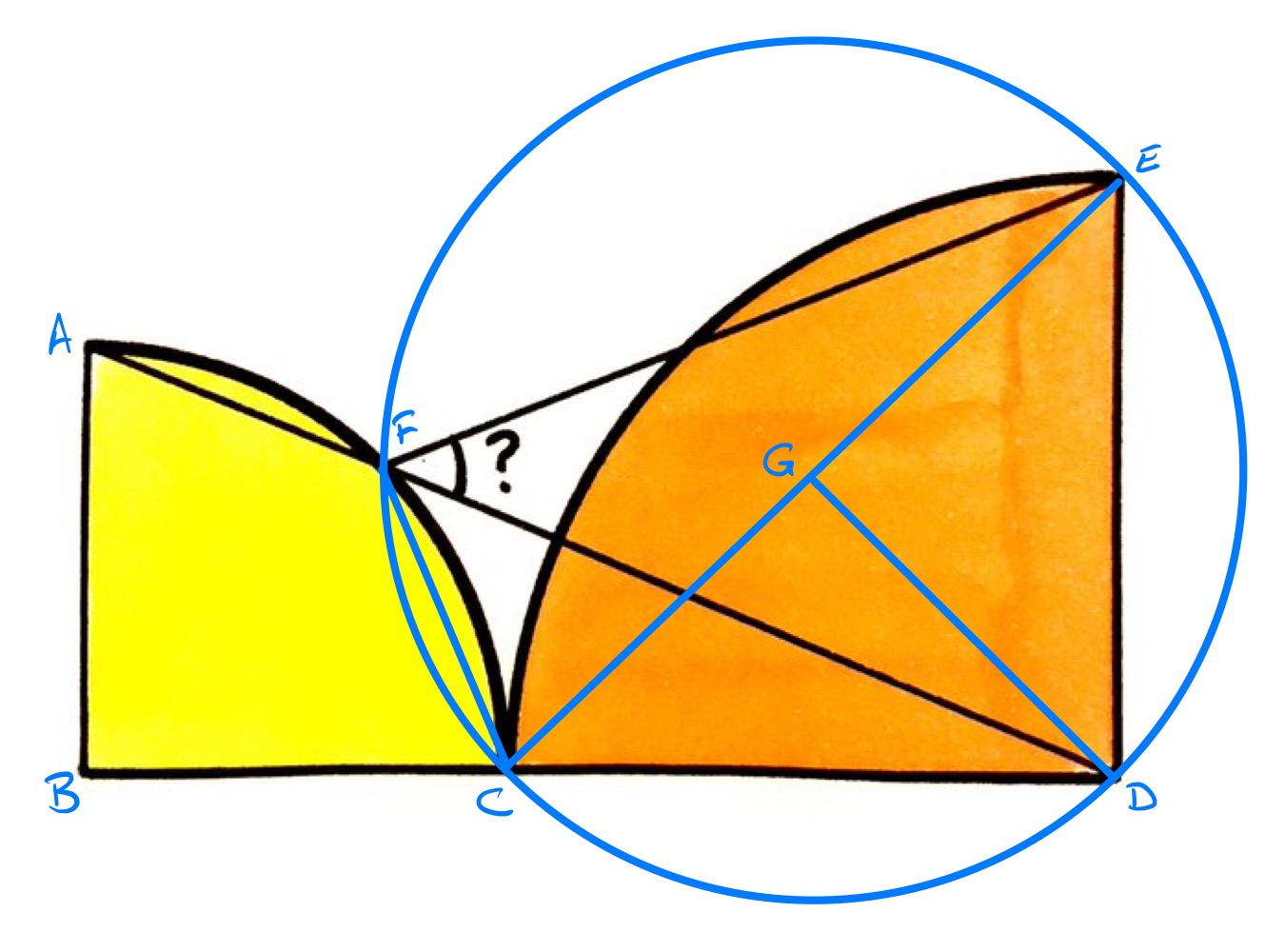
With the points labelled as above, the blue circle has centre $G$ and passes through $C$, $D$, and $E$. The point $F$ will end up lying on this circle, but this needs to be shown.

The reflex angle $A \hat{B} C$ is $270^\circ$, so since the angle at the circumference is half the angle at the centre, angle $A \hat{F} C$ is $135^\circ$. Then from angles at a point on a straight line, angle $C \hat{F} D$ is $45^\circ$. This is the same as angle $C \hat{E} D$ and so from the converse to angles in the same segment being equal, $F$ lies on the same circle as $E$, $C$, and $D$.

Finally, since angles in the same segment are equal, angle $D \hat{F} E$ is the same as angle $D \hat{C} E$, which is $45^\circ$. Hence angle $D \hat{F} E$ is $45^\circ$.