Notes
two quarter circles in a square solution
Solution to the Two Quarter Circles in a Square Puzzle
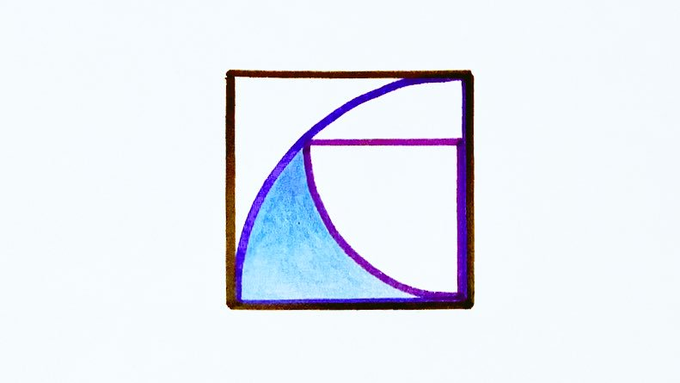
Two quarter circles inside a square. What fraction is shaded?
Solution by Area of a Circle and Area of a Triangle
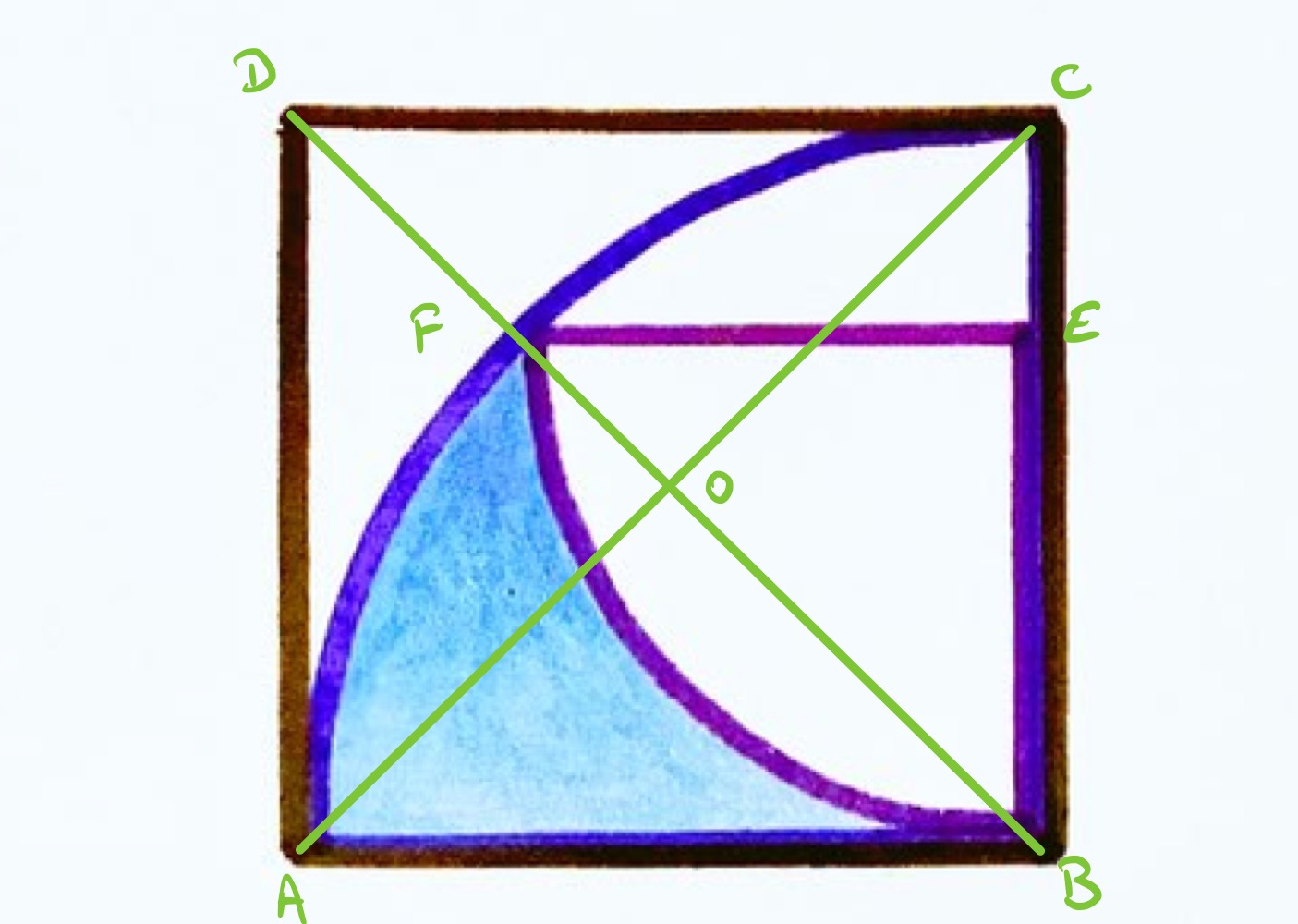
As this is a question about what fraction of the square is shaded, let us set the side length of the square to .
With the points labelled as above, the sector is an eighth of a circle with centre and radius , so its area is .
As is on the quarter circle with centre , the line segment is the same length as . Triangle is an isosceles right-angled triangle and so the length of is . The area of the quarter circle is therefore:
The area of triangle is then so the segment cut out from the smaller quarter circle by the chord has area .
The shaded area is therefore:
And so the shaded area is one quarter of the square.