Notes
two quarter circles in a semi-circle solution
Solution to the Two Quarter Circles in a Semi-Circle Puzzle
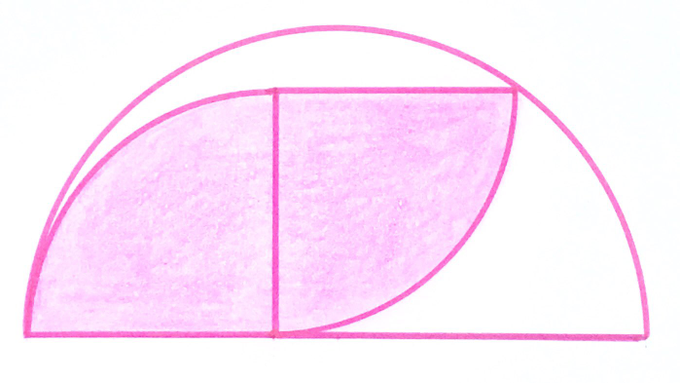
What fraction of the semicircle do these quarter circles cover?
Solution by Similar Triangles and Properties of Chords
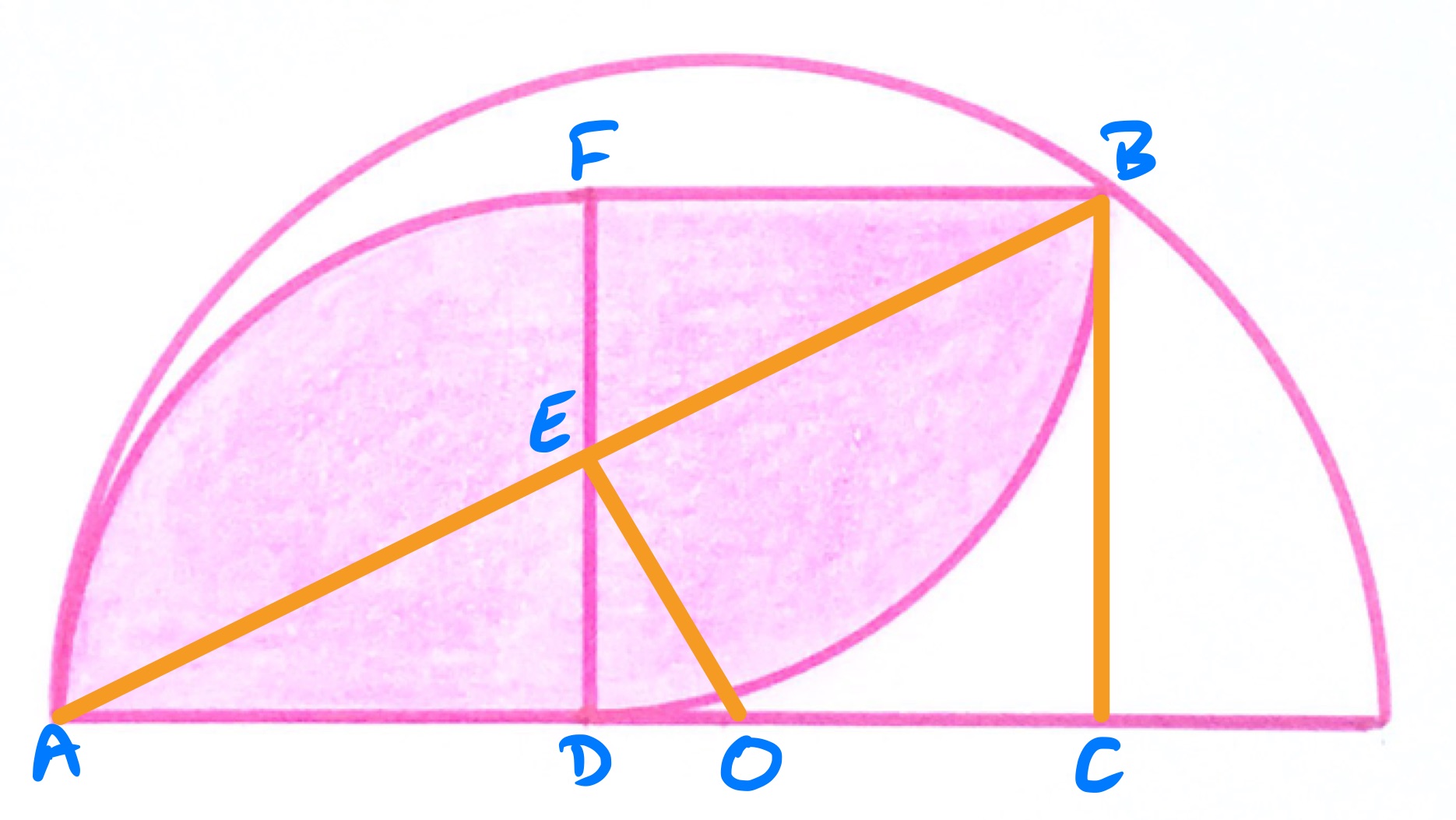
In the above diagram, the point is the centre of the circle, the point is where the chord intersects the line up from , and is so that is perpendicular to the diameter.
As the quarter circles have the same radius, is the midpoint of and so is the midpoint of . The line segment is therefore perpendicular to the chord . This means that angles and add up to , but also angles and add up to since angles in a triangle add up to , so angle is equal to angle . As angle is a right-angle, this establishes triangle as similar to triangle .
As is the midpoint of , it is also the midpoint of and so has length half that of . By similarity, therefore, has length half that of and so a quarter of that of . The length of is therefore of that of , equivalently the length of is of .
The area of the quarter circles is and of the semi-circle is . The ratio of these areas is therefore .