Notes
two quarter circles in a rectangle solution
Solution to the Two Quarter Circles in a Rectangle Puzzle
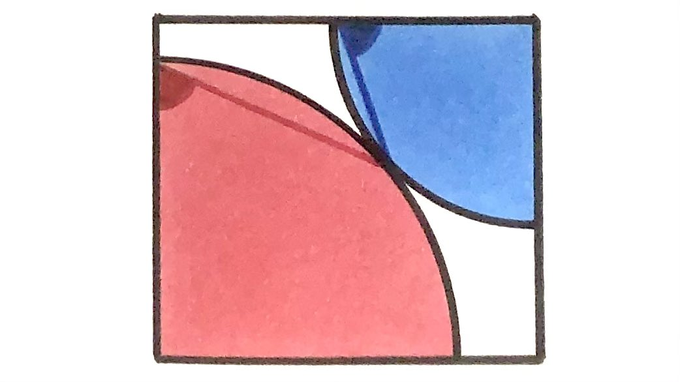
What’s the sum of these two angles?
Solution by Isosceles Triangles, Angles in a Triangle, and Properties of Circles
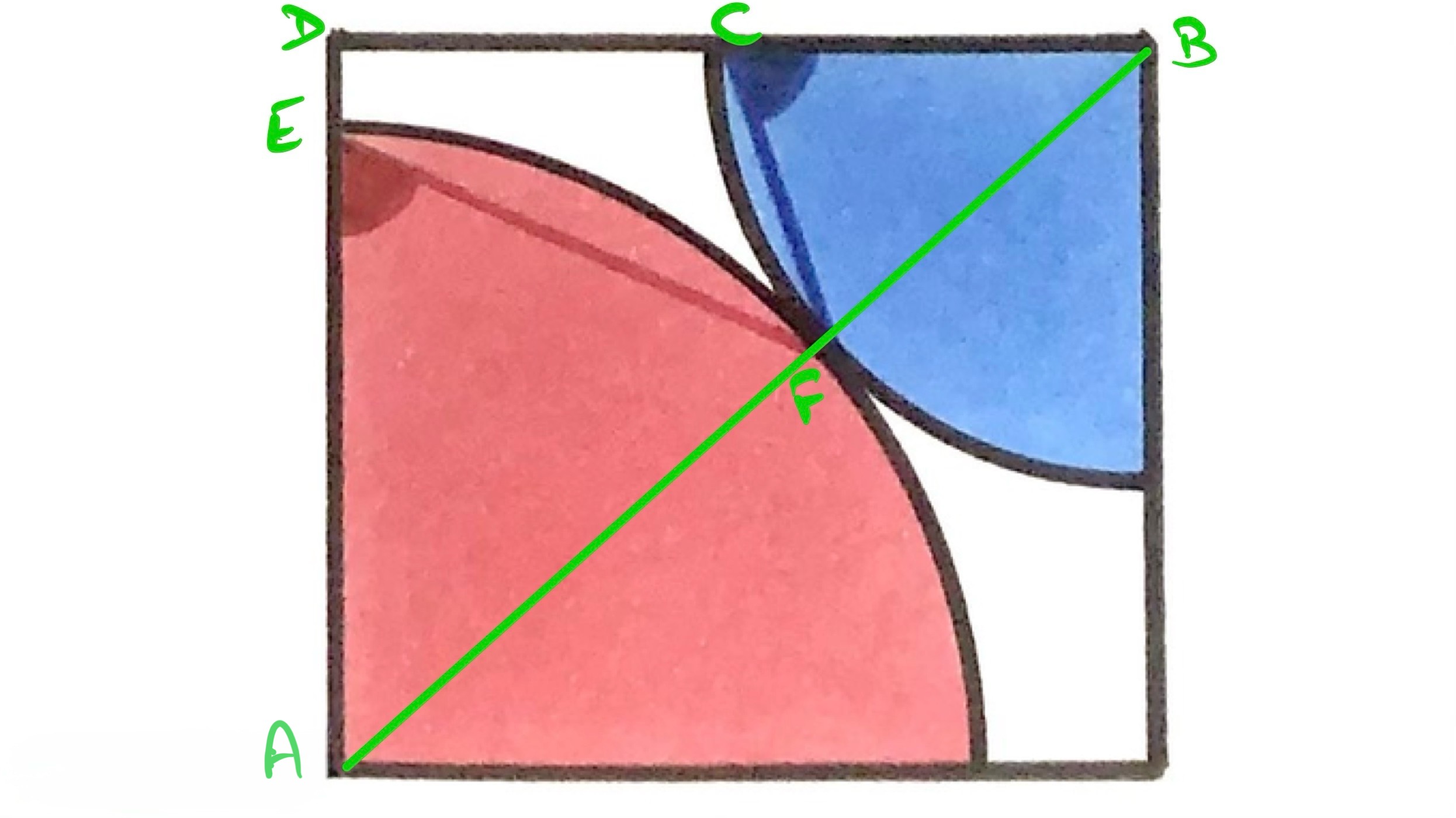
With the points labelled as above, the point where the quarter circles touch, , lies on the line between their centres, so is a straight line and is a diagonal of the rectangle.
As is the centre of the red quarter circle, triangle is isosceles and therefore angle is the same as angle . Similarly, angle is the same as angle .
Since angles in a triangle add up to , the angles in triangle and in triangle add up together to . So
Then also is a triangle and angle is a right-angle, so , meaning that: