Notes
two quarter circles in a rectangle in a semi-circle solution
Solution to the Two Quarter Circles in a Rectangle in a Semi-Circle Puzzle
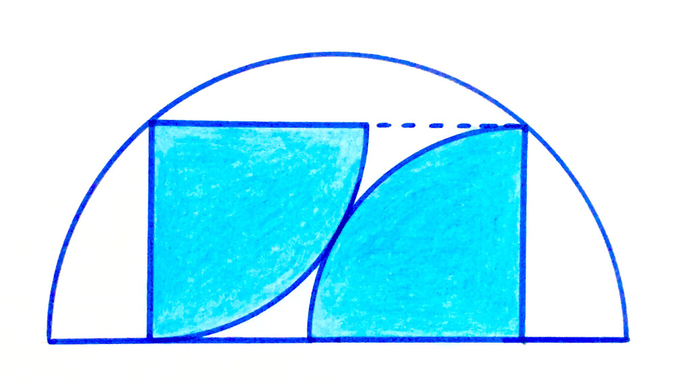
Two quarter circles in a semicircle. What fraction is shaded?
Solution by Pythagoras' theorem and Area Scale Factor
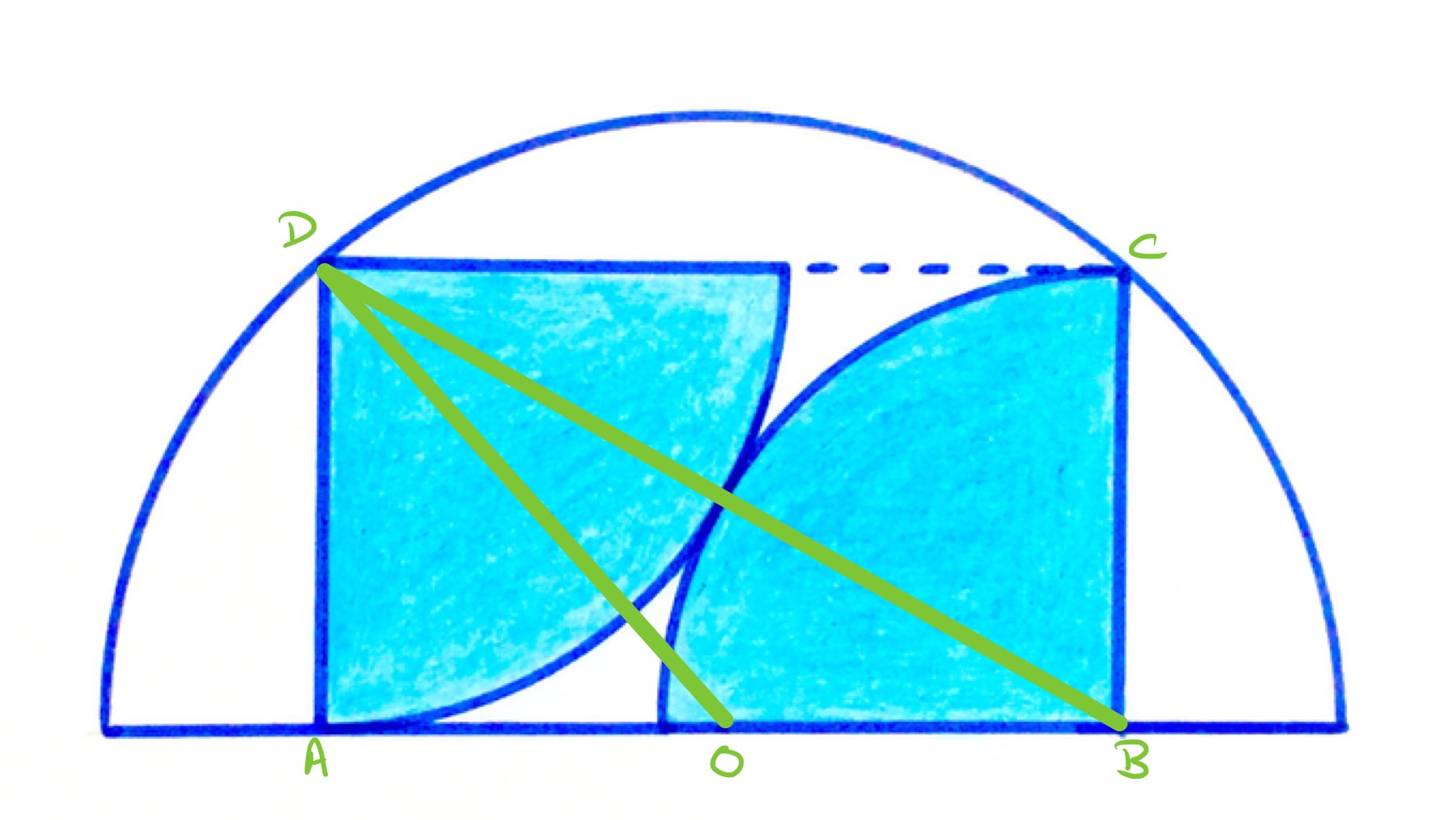
In the above diagram, point is the centre of the larger semi-circle.
The line segment passes through the point where the two quarter circles touch so its length is twice the radius of the quarter circles. Line segment is a radius, so triangle is a right-angled triangle with hypotenuse twice the length of one of its sides. Pythagoras' theorem then shows that has length times the length of . Then is half this, so applying Pythagoras' theorem to triangle shows that is times the length of . Since area scales as the square of the length scale factor, the outer semi-circle is then the area of the two quarter circles, so the shaded region is ths of the total region.