Notes
two quarter circles and a semi-circle solution
Solution to the Two Quarter Circles and a Semi-Circle Puzzle
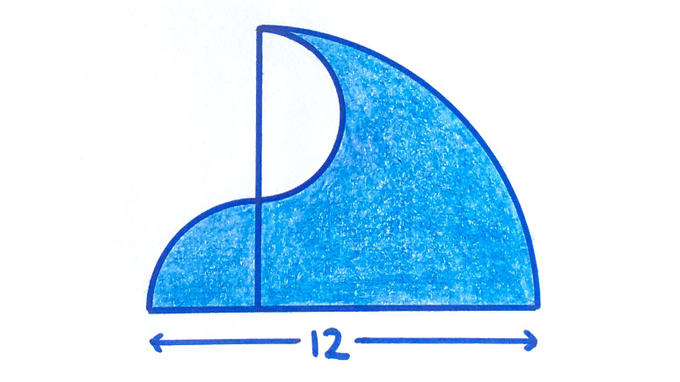
Two quarter circles and a semicircle. What’s the shaded area?
Solution by Circle Area
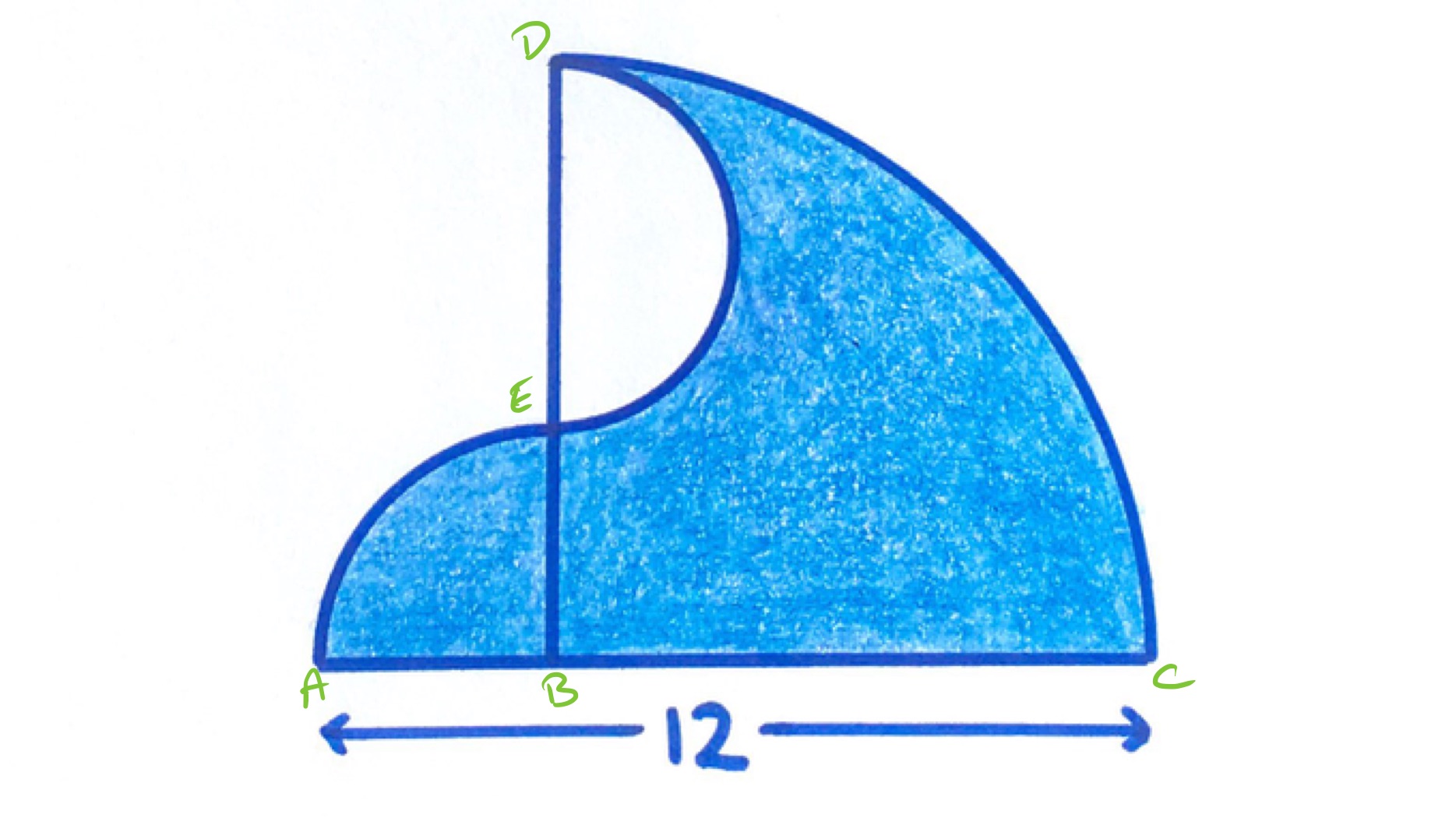
With the points labelled as above, let be the length of , the length of and half the distance of . Then , , and are the radii of the three circles. The diagram gives , and .
The shaded area is given by:
From , . So:
So the shaded area is given by: .
Solution by Invariance Principle
There are two special cases,in the first the two quarter circles are the same size and the cut out semi-circle has no area. In the second, the smaller quarter circle has no size.
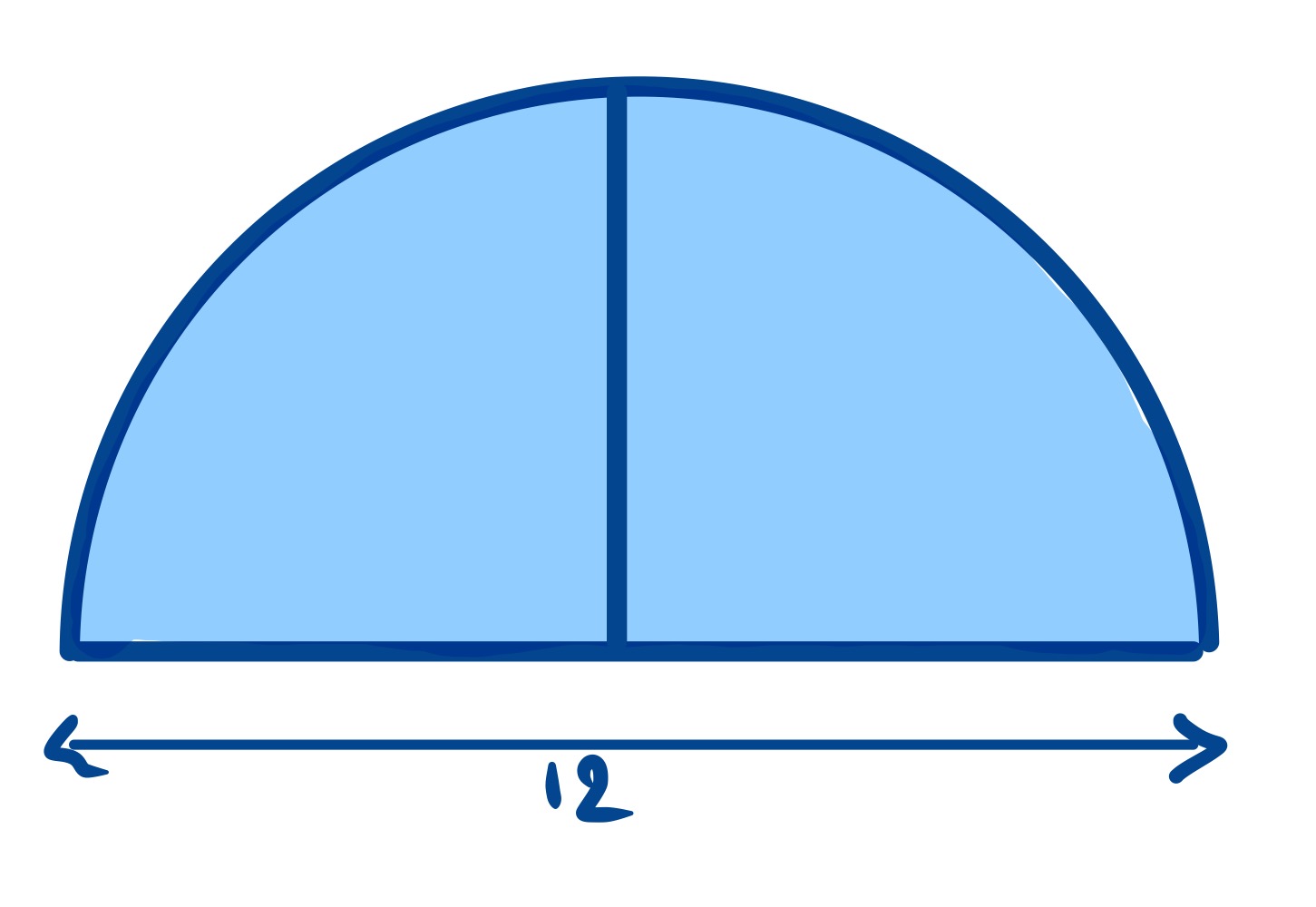
The area here is .
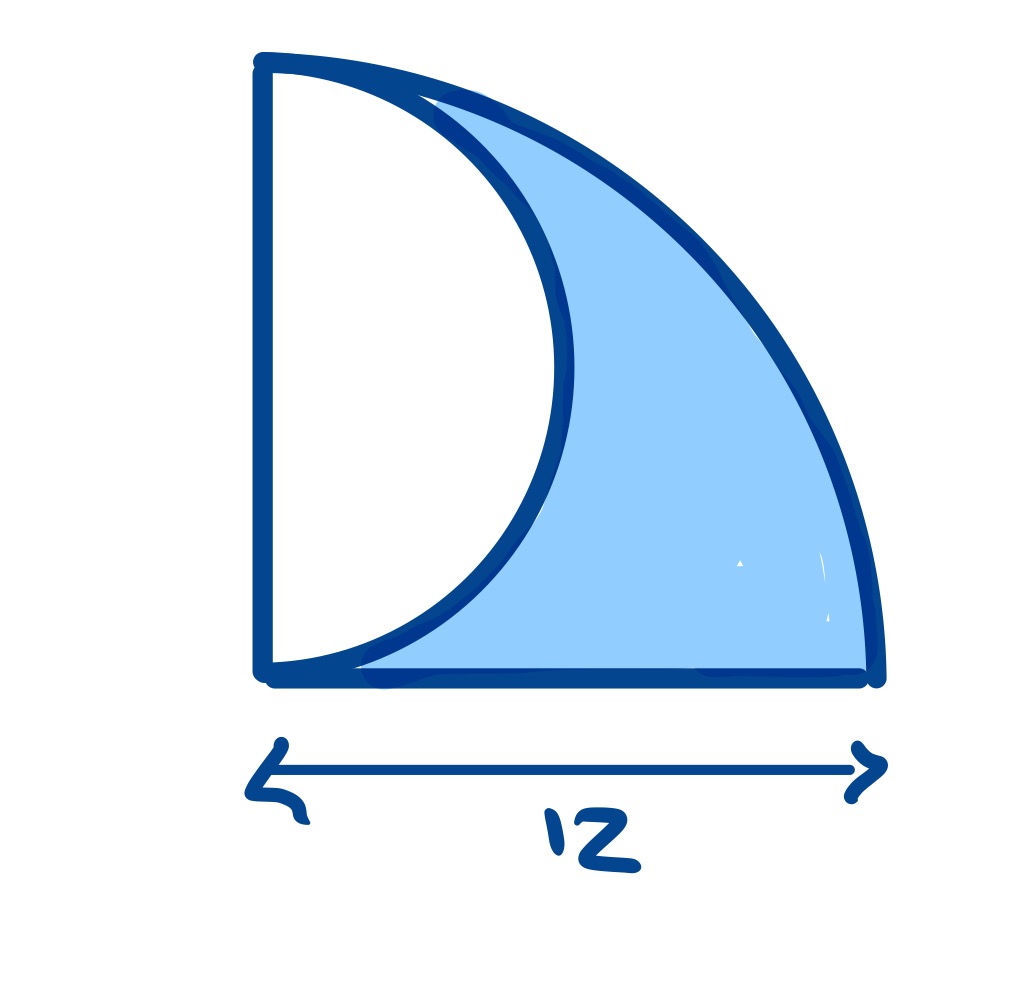
The area here is .