Notes
two quarter circles and a semi-circle ii solution

Solution to the Two Quarter Circles and a Semi-Circle II Puzzle

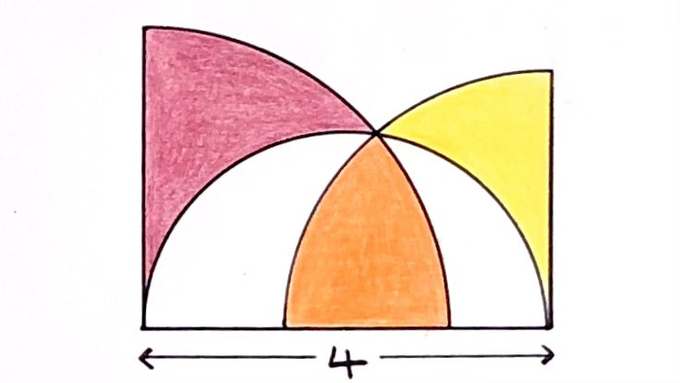
Two Quarter Circles and a Semi-Circle II

Two quarter circles and a semicircle. What’s the total shaded area?

Solution by Circle Area, Angle in a Semi-Circle, and Pythagoras' Theorem

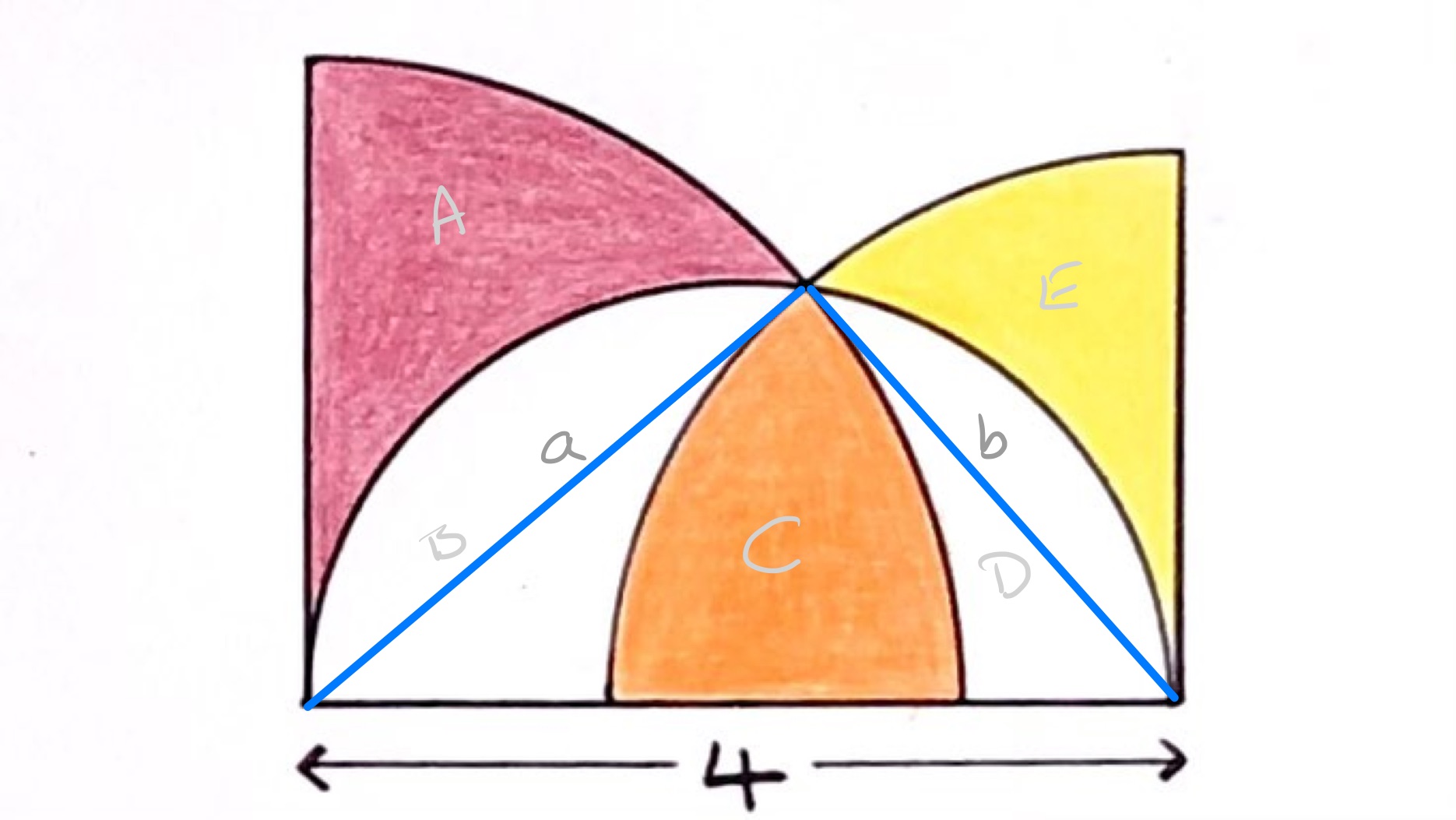
Two quarter circles and a semi-circle labelled

With the diagram annotated as above, the left-hand quarter circle has area:

\frac{1}{4} \pi a^2

and the right-hand one:

\frac{1}{4} \pi b^2

The area of the semi-circle is:

\frac{1}{2} \pi 2^2

The triangle formed by the segments is a right-angled triangle as the angle in a semi-circle is a right-angle. Therefore, by Pythagoras' theorem:

a^2 + b^2 = 4^2

In terms of the labelled areas, the left-hand quarter circle is $A + B + C$ , the right-hand quarter circle is $C + D + E$ , and the semi-circle is $B + C + D$ . The shaded area is $A + C + E$ which can be written as:

A + C + E = (A + B + C) + (C + D + E) - (B + C + D)

Putting these together, the shaded area is given by:

\begin{aligned} A + C + E &= \frac{1}{4} \pi a^2 + \frac{1}{4} \pi b^2 - \frac{1}{2} \pi 2^2 \\ &= \frac{1}{4} \pi (a^2 + b^2) - \frac{1}{2} \pi 2^2 \\ &= \frac{1}{4} \pi 4^2 - \frac{1}{2} \pi 2^2 \\ &= 4 \pi - 2 \pi \\ &= 2 \pi \end{aligned}

Created on June 10, 2021 12:07:44 by Andrew Stacey

Notes two quarter circles and a semi-circle ii solution

Solution to the Two Quarter Circles and a Semi-Circle II Puzzle

Solution by Circle Area, Angle in a Semi-Circle, and Pythagoras' Theorem

Notes
two quarter circles and a semi-circle ii solution