Notes
two perpendicular equilateral triangles solution
Solution to the Two Perpendicular Equilateral Triangles Puzzle
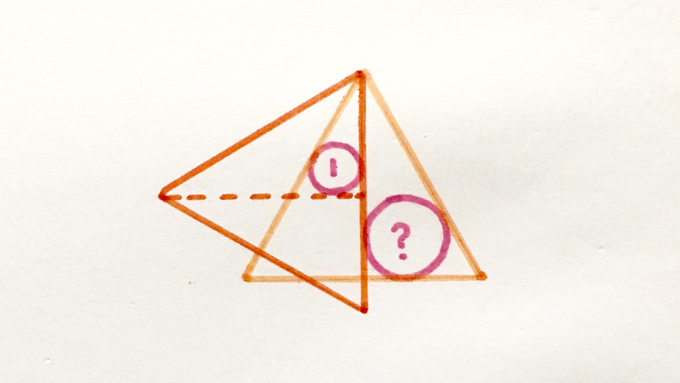
The medians of these two equilateral triangles are perpendicular. What’s the area of the larger circle?
Note: for this to be a well-defined problem, the equilateral triangles are assumed to be the same size.
Solution by Similar Triangles and Lengths in an Equilateral Triangle
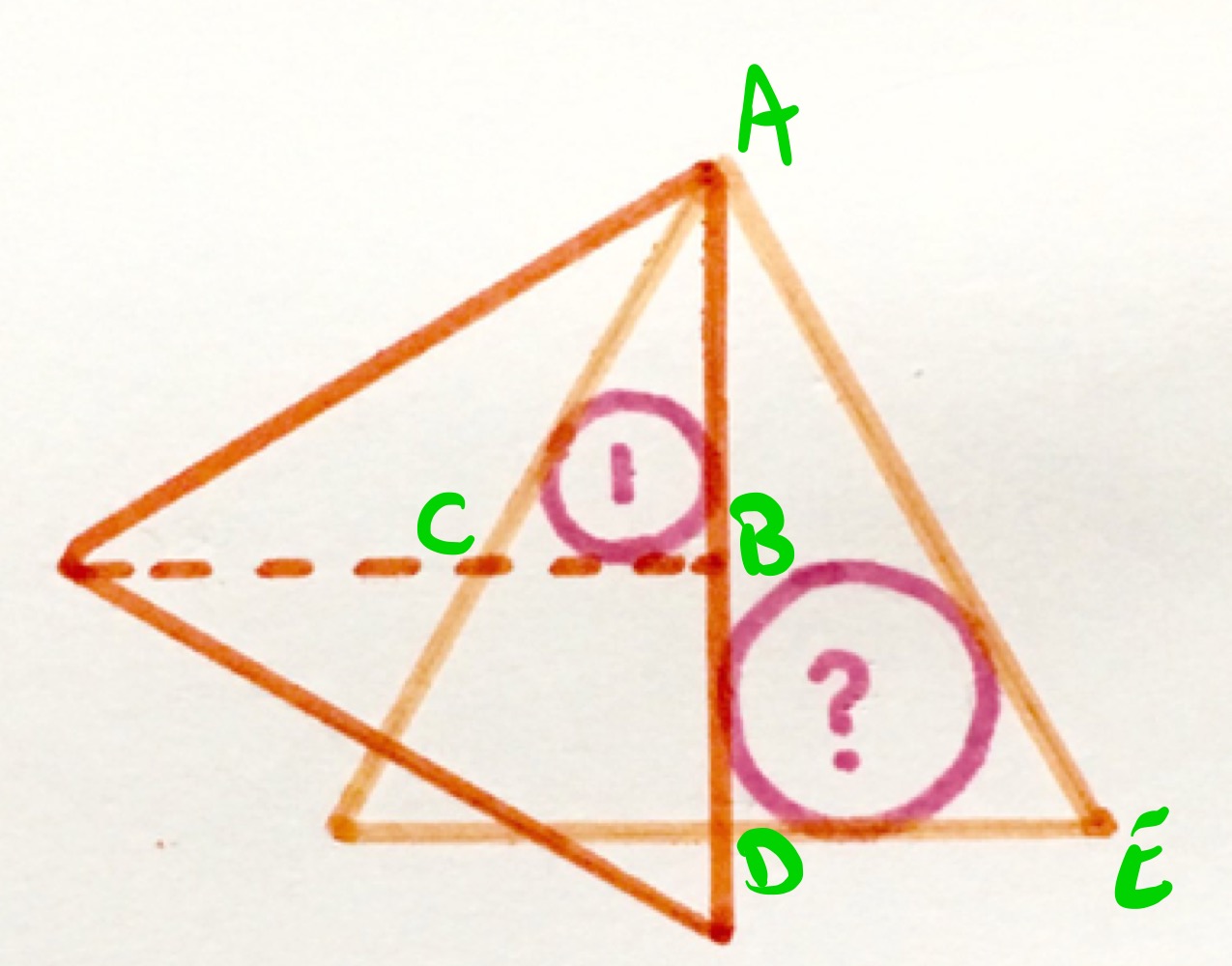
With the points labelled as above, triangles and are similar, and the scaling also takes one circle to the other. The scale factor is found by comparing the lengths of and . That of is half the side length of one of the equilateral triangles while that of is of the side length. So the ratio is . The area scale factor is therefore and so the area of the larger circle is .