Notes
two overlapping triangles solution
Solution to the Two Overlapping Triangles Puzzle
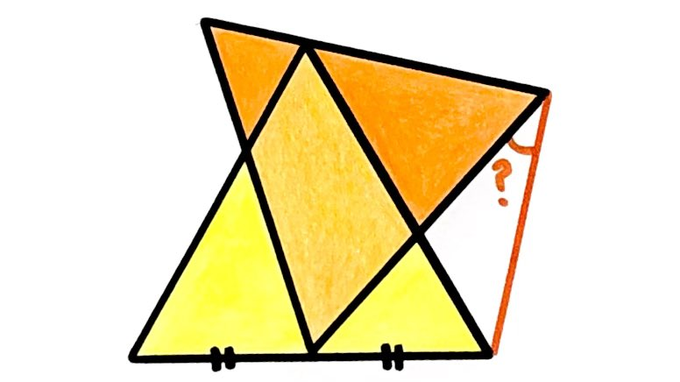
Two equilateral triangles. What’s the angle?
Solution by Similar Triangles
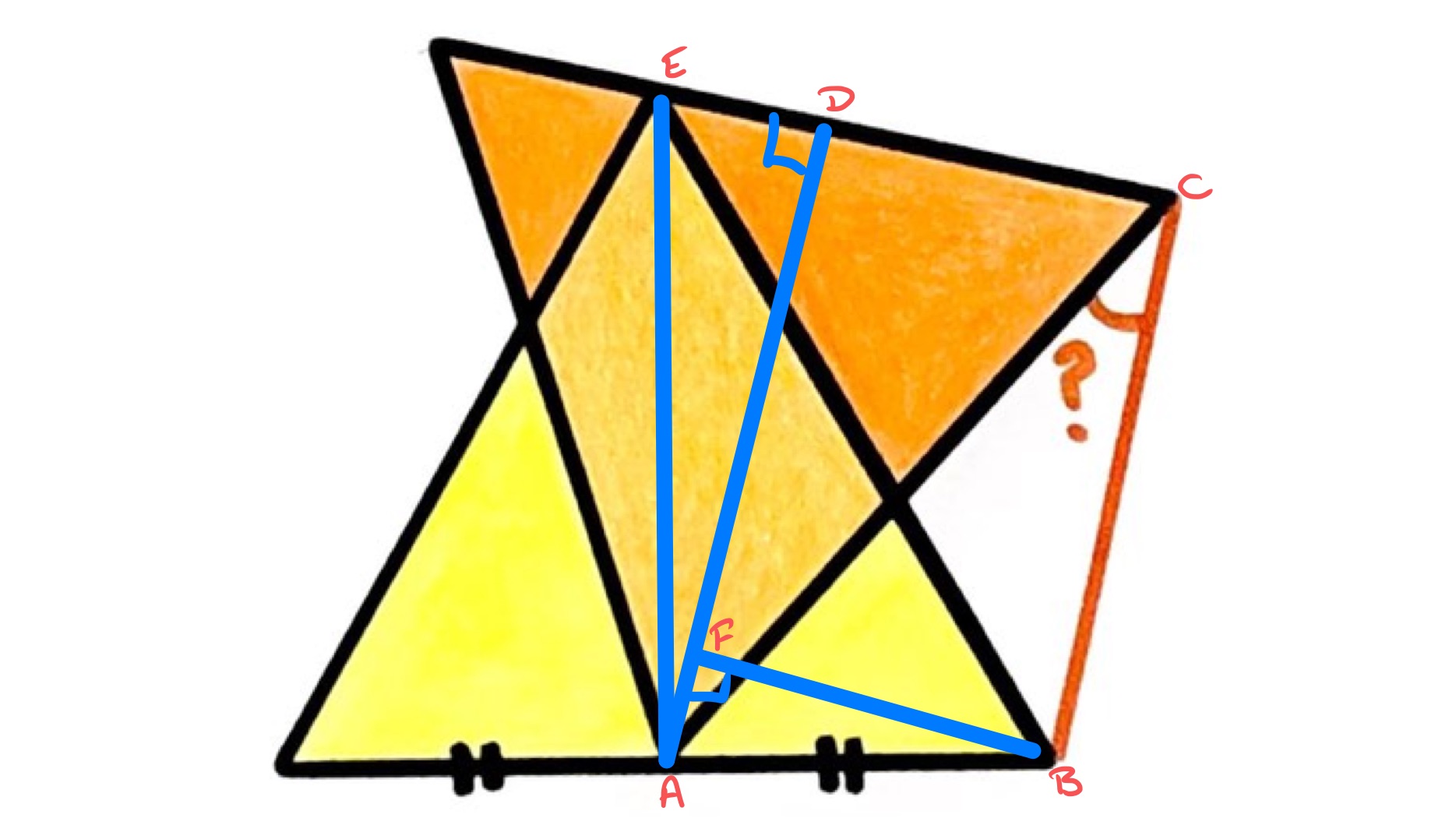
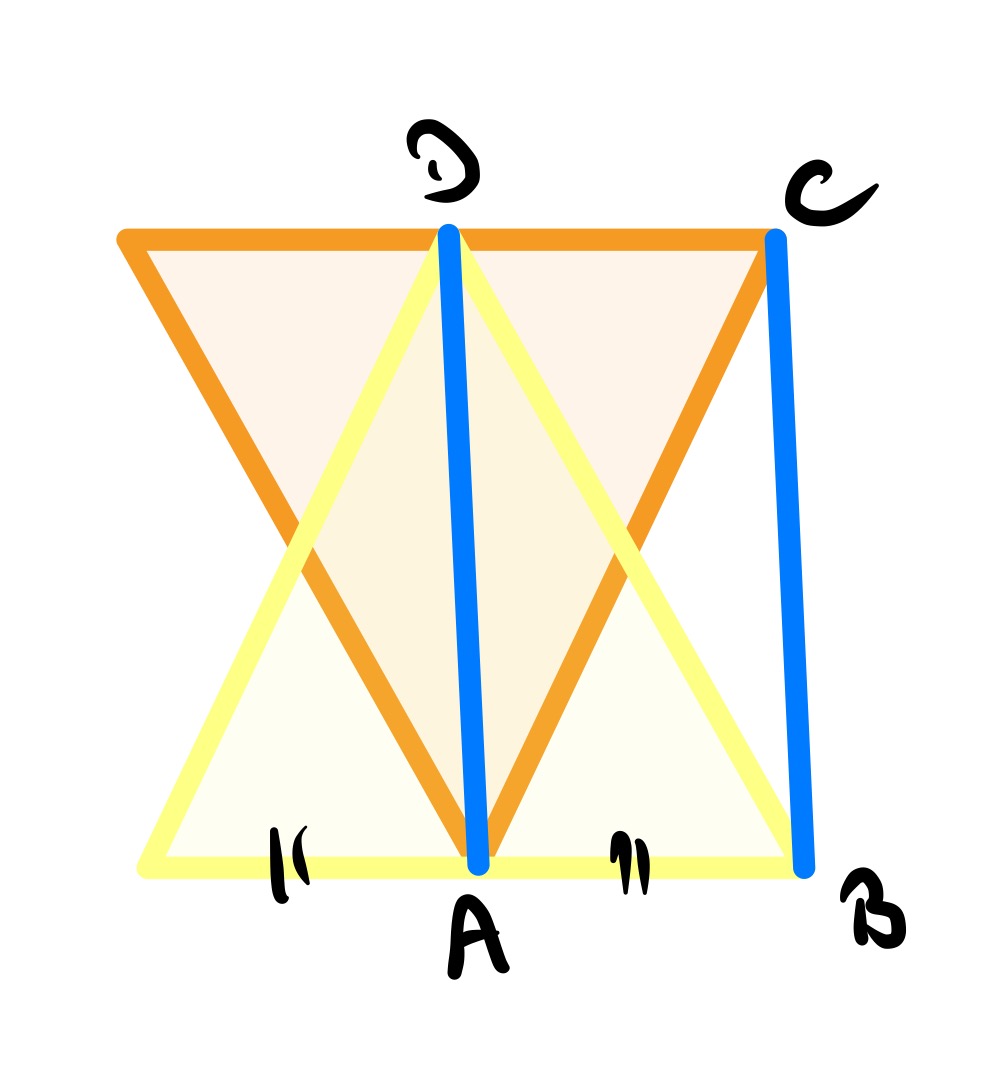
In the above diagram, is the midpoint of the side of the orange triangle and is so that angle is a right-angle. Since angle is a right-angle, angles and add up to a right-angle, and so angles and are equal. This implies that triangles and are similar. From this, the ratio of lengths is the same as . Since is half the side length of the equilateral triangle of which is the height, has length half the side length of an equilateral triangle of which is the height. Therefore and have the same length and so is a rectangle. Since angle is , this leave angle as .
Solution by Angles in the same segment and Angle at the centre is twice the angle at the circumference
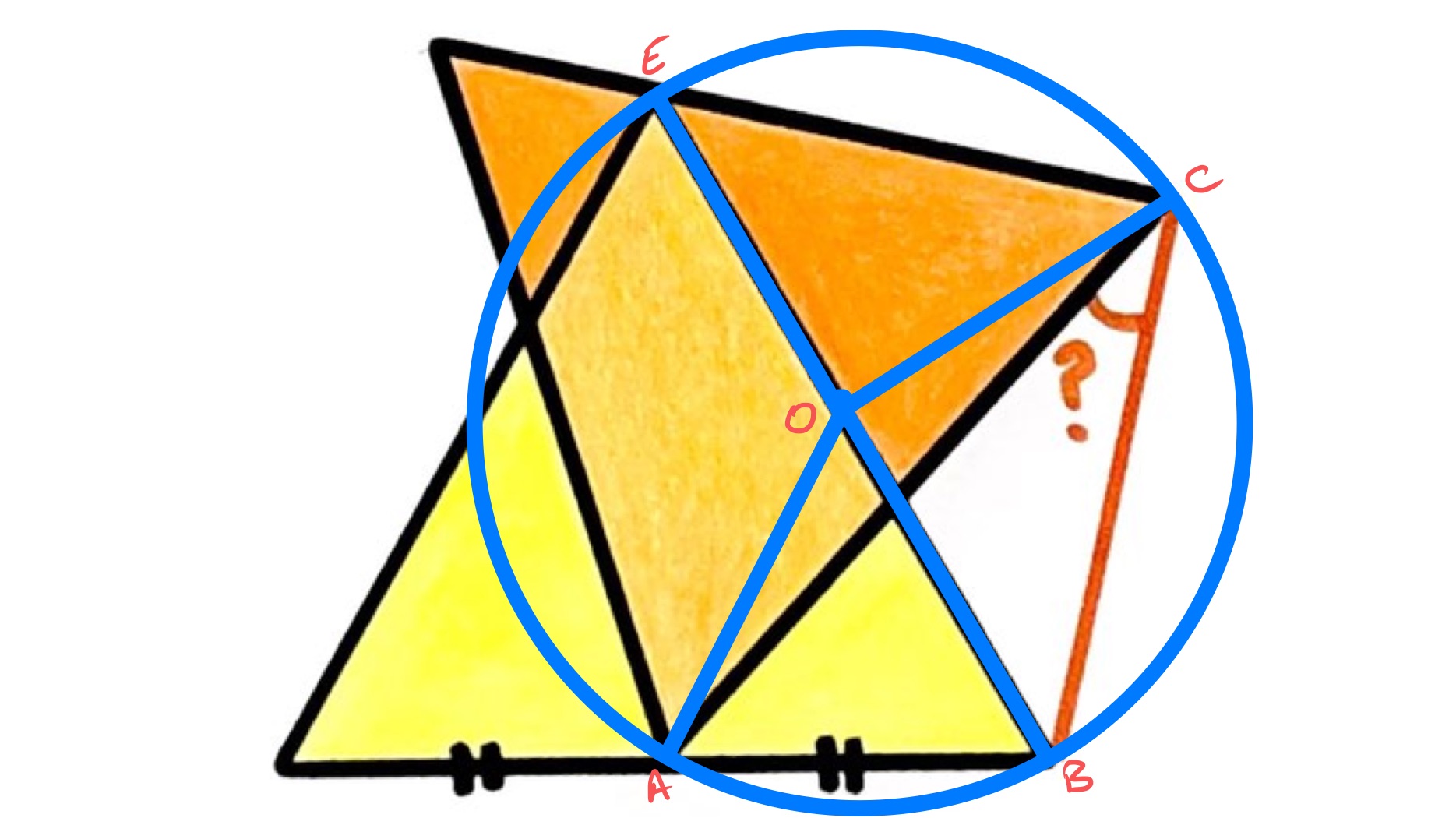
In the above diagram, point is the midpoint of the side , so the circle centred at that passes through also passes through . As is the midpoint of the base of the yellow equilateral triangle, is the same length as and so the circle also passes through . Angle is which is the same as angle , so by the result that angles in the same segment are equal, also lies on the circle. Therefore since the angle at the centre is twice the angle at the circumference, angle is half of angle which is . Hence angle .
Solution by Transformations
For this solution, view the orange triangle as fixed and the yellow triangle as variable. It is determined by the point which is free to move on the line that extends the top side of the orange triangle. The point is obtained from by a rotation clockwise about the point (which is fixed relative to the orange triangle) and scaling by . Therefore, moves on a straight line (relative to the orange triangle). To see where this straight line is, consider two special cases.
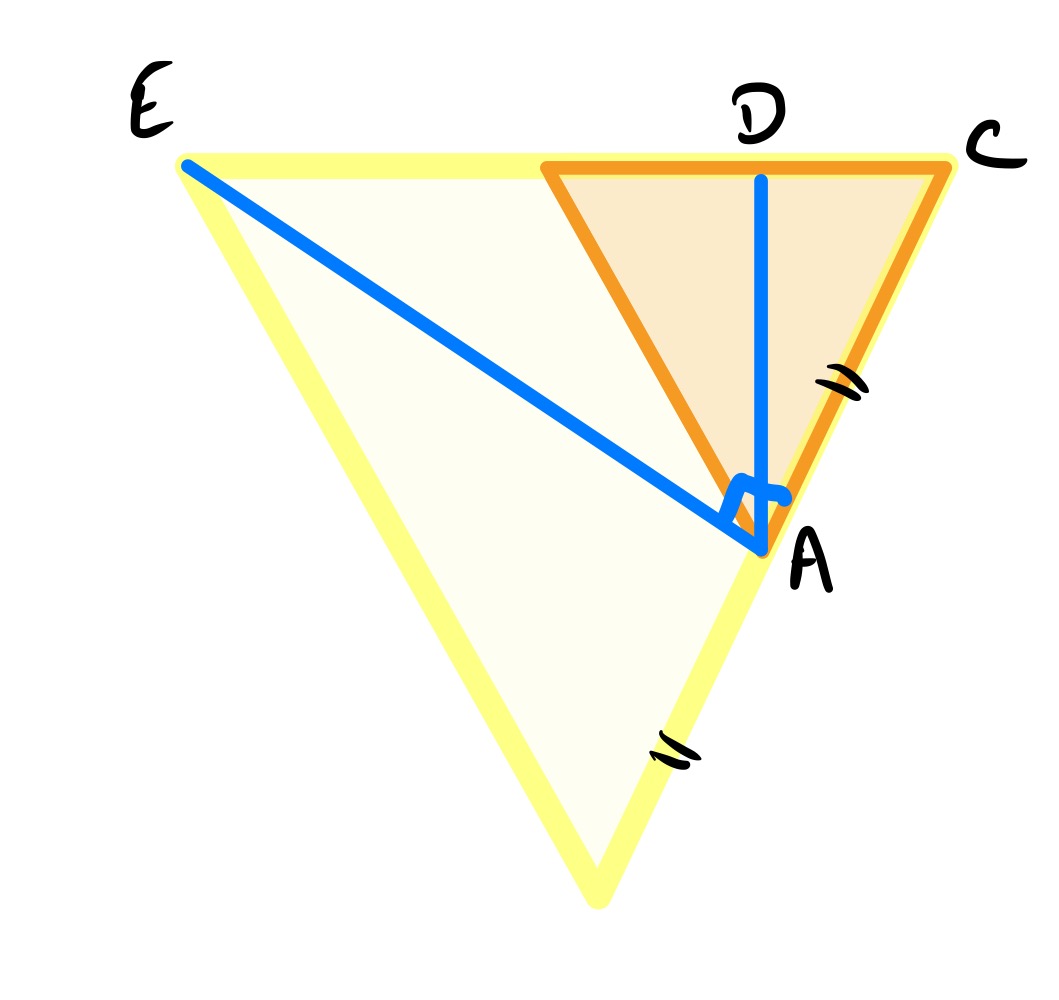
In this case, is at a point so that lies along . This is also characterised by the fact that angle . In this case, coincides with .
The second special case is where is at . In this diagram, angle is evidently a right-angle.
So the line that moves on passes through at right-angles to the line . Since angle , this shows that angle .
Solution by Invariance Principle
The diagram for the second special case above can also be used to demonstrate the solution using the strong invariance principle.