Notes
two overlapping triangles ii solution
Solution to the Two Overlapping Triangles (II) Puzzle
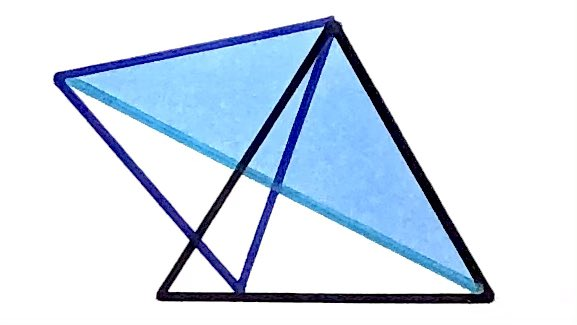
The largest of these two equilateral triangles has area . What’s the blue area?
Solution by Calculating Lengths
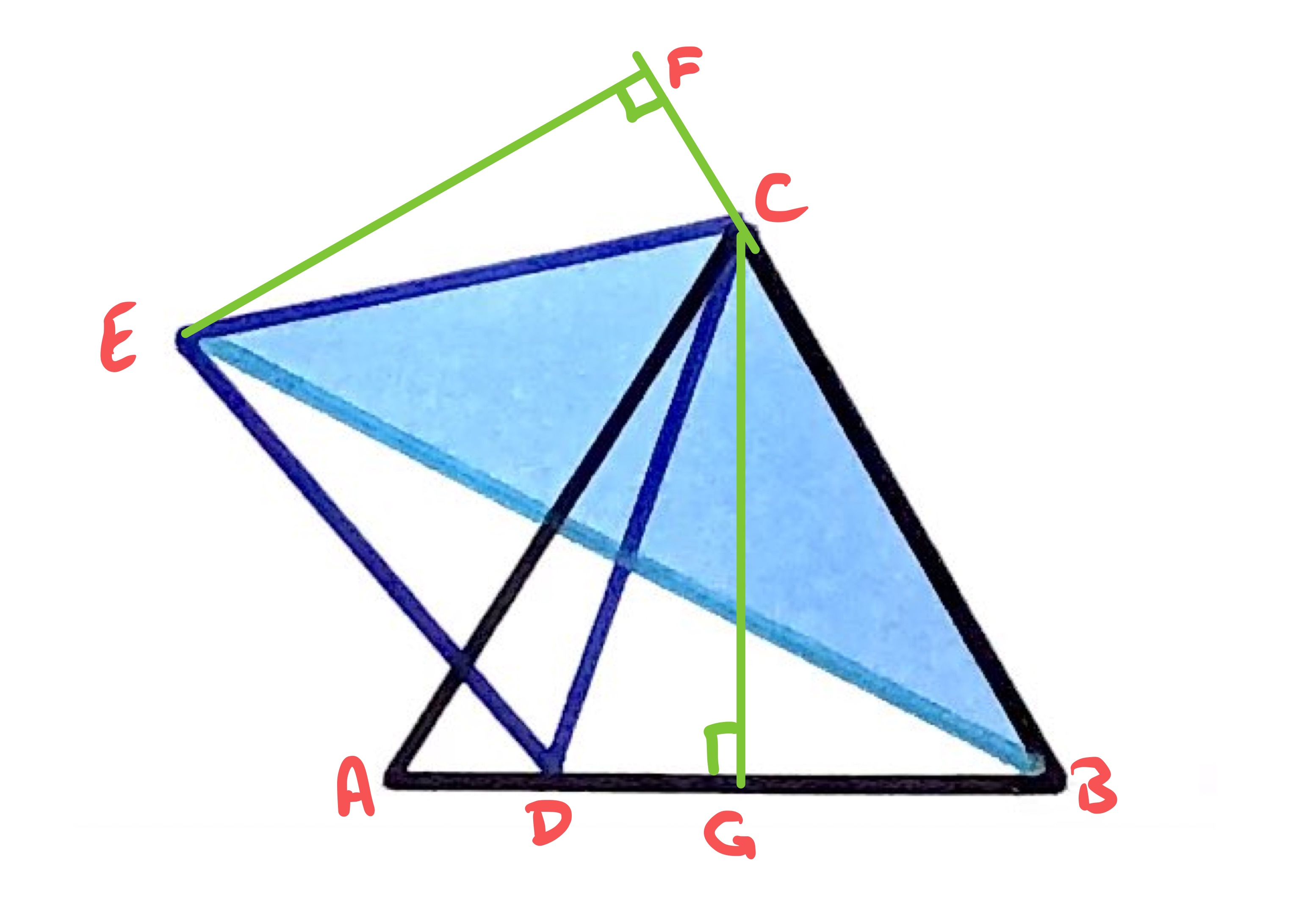
The blue area is a triangle, so to calculate its area we can start with picking a side to be the “base”. The side coincides with one of the sides of the equilateral triangle whose area is given, so that seems a reasonable side to pick.
The perpendicular height of the triangle from this base is the length . The triangle is congruent to triangle , meaning that length . This is the height of the equilateral triangle above . As the triangle is equilateral, and so the two triangles have the same base and perpendicular height, and thus the same area.
Solution by Symmetry
There is a strategy for solving this which exploits symmetry. To use this, draw a copy of the larger triangle rotated by clockwise.
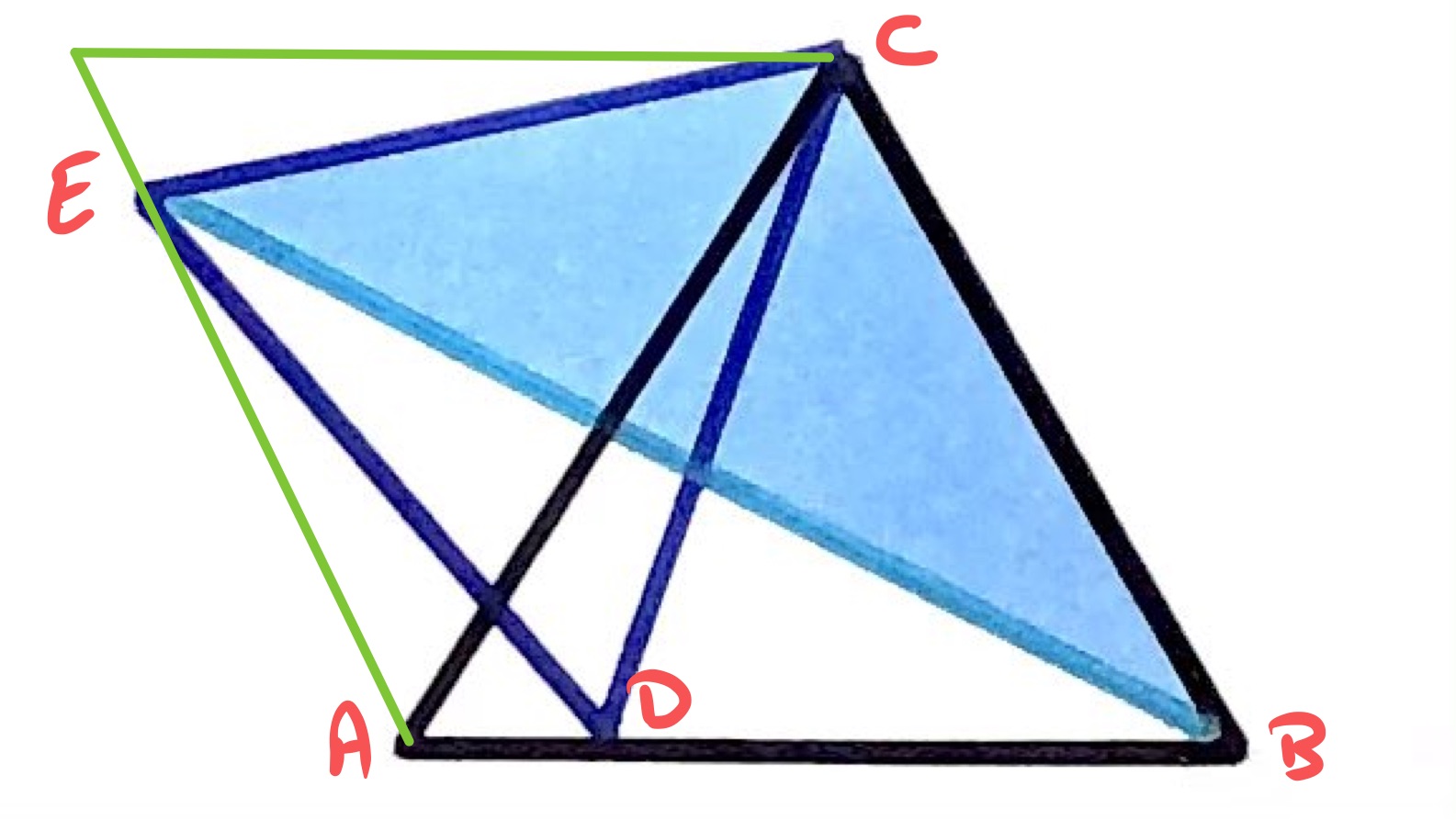
The side of the smaller triangle becomes the side , as the smaller triangle is also equilateral. The point lies on the side of the new triangle which is parallel to the side of the original triangle. This then establishes the perpendicular height above of the blue area as being the height of the larger triangle above the same side, and therefore that the blue area has the same area as the larger triangle.
Solution by the Invariance Principle
Both the weak and strong Invariance Principles can be used to solve this problem. The position of along the side is not fixed and so could be anywhere along that edge.
For the strong principle, we can look at either of the extremes. If coincides with then the blue area is exactly the same as the larger triangle and so has area . If coincides with then the “smaller” triangle is a copy of the original triangle and the blue area then consists of two halves of that triangle, and so has area .
The weak principle says that the area is independent of the position of and so the height of the blue area, which is the perpendicular distance of above , must be constant. This means that as moves on , the point moves on a straight line parallel to that passes through . Drawing in this line leads to the symmetry solution above.