Notes
two overlapping squares iii solution
Solution to the Two Overlapping Squares III Puzzle
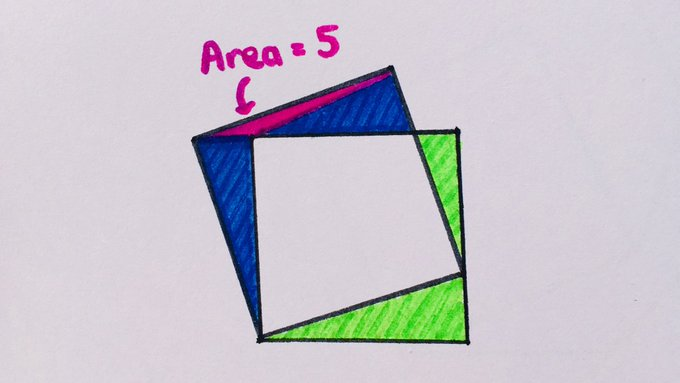
Is more of this design green or blue (and by how much)?
Solution by Properties of Area and Transformations
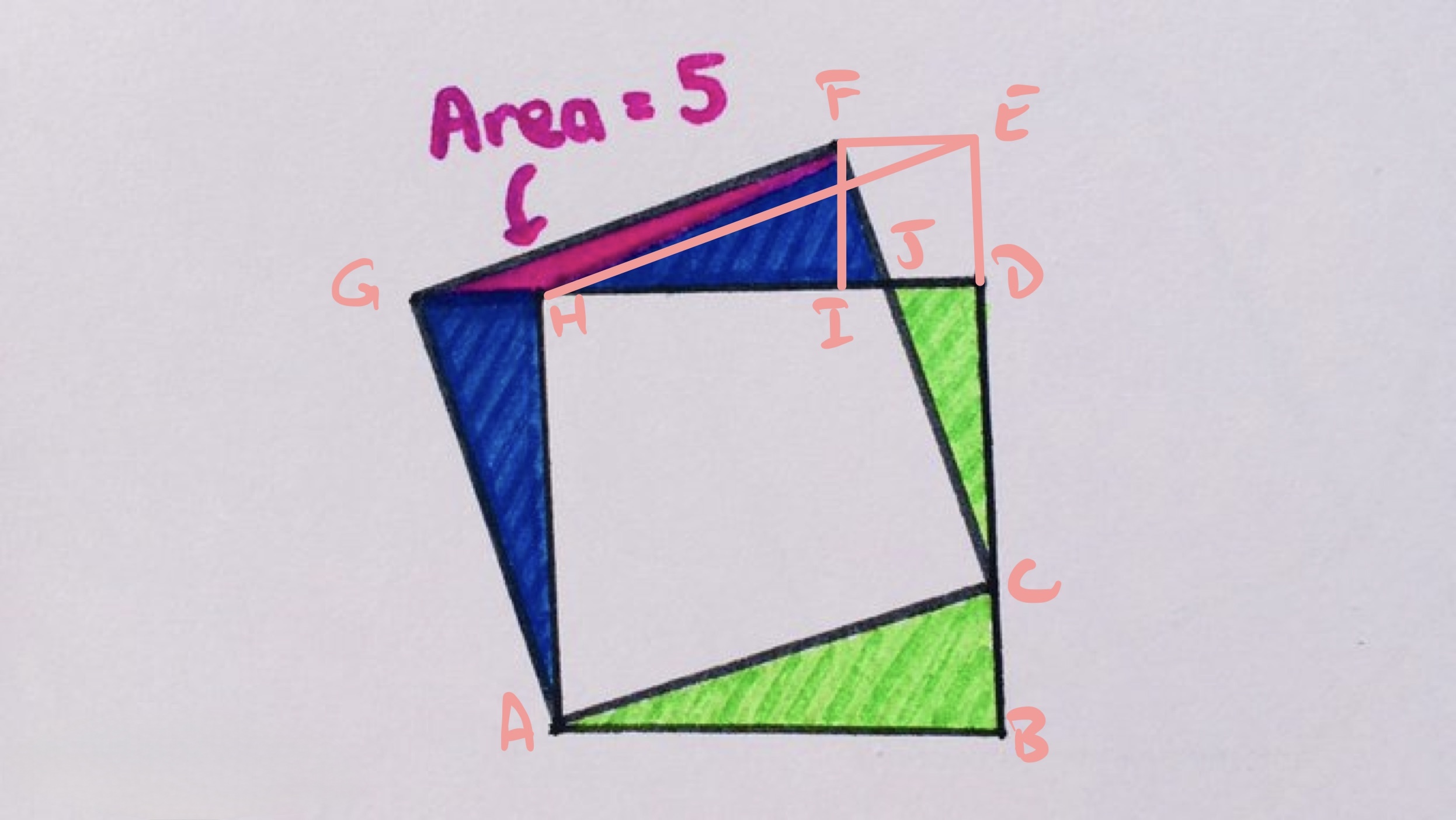
Label the points as above. To compare the blue and green areas, we add in to both the quadrilateral . In this, the point is such that is perpendicular to and is on the continuation of so that is perpendicular to .
Rotating anticlockwise about takes to and to , therefore triangles and are congruent and, in particular, have the same area.
This also means that angle is and so is a continuation of , so is a straight line.
Translating along to takes to and onto the line . Since angle is , and angle is also , this translation takes to and so triangles and are also congruent. Further translating it so that translates to takes onto , establishing those as congruent.
A similar argument shows that triangle is congruent to via the translation that takes to and to . Since triangles and are congruent, this means that triangles and are also congruent.
This means that by including the quadrilateral and considering it a part of both the blue and green regions means that they can be matched except for the triangle which is the excess blue.
This triangle is half of the parallelogram and so its area is the same as the pink region, which is .
Hence the blue area is larger than the green by .
Solution by Invariance Principle
The angle at which the squares are to each other can be varied, with the restriction that stay on the edge . Putting it at doesn’t work since then the squares overlap exactly and all the regions are empty (even the one set at ). That leaves putting it at which results in the diagram below.
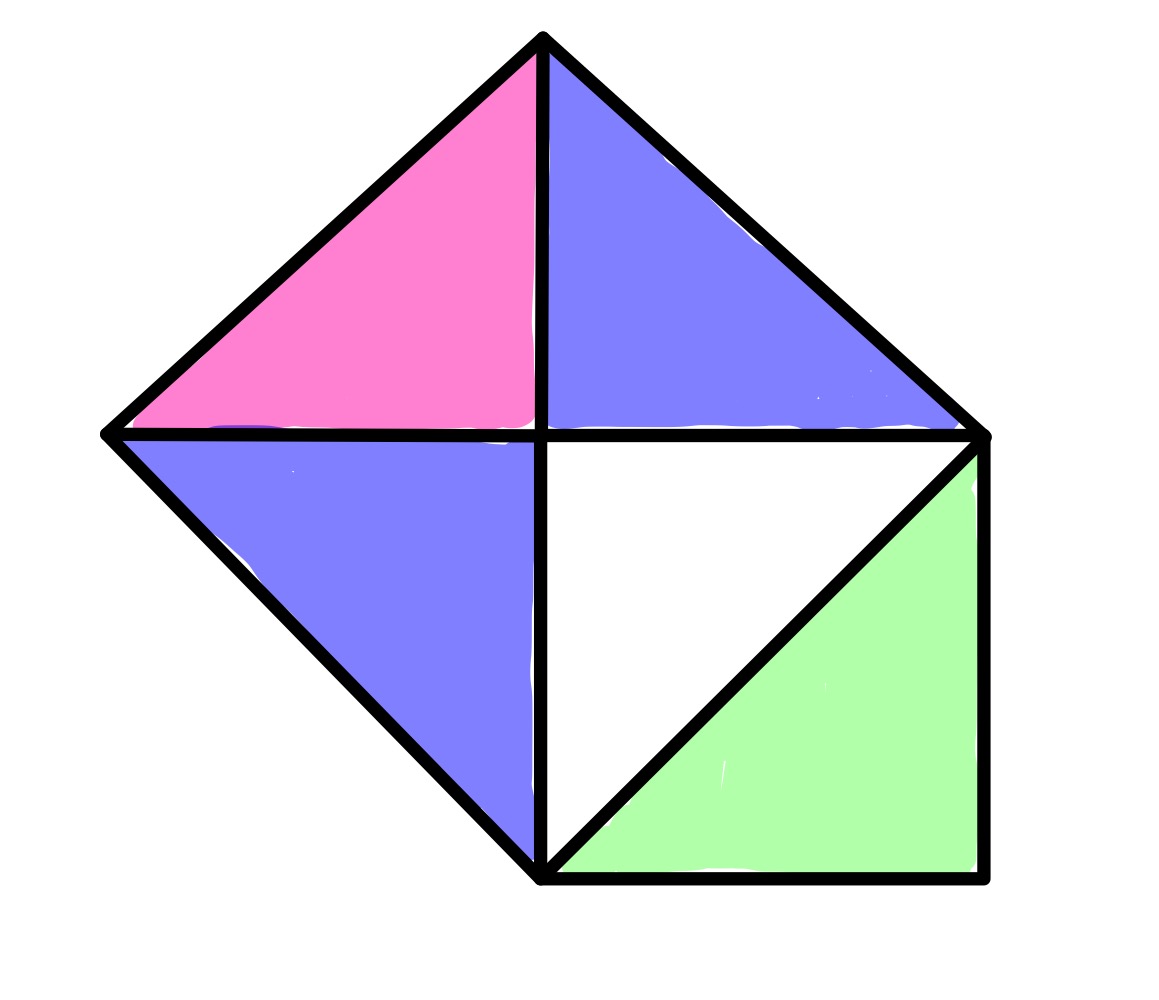
In this version of the diagram, the triangles are all congruent so the blue region is one triangle more than the green, and that triangle is the same as the pink so has area .