Notes
two overlapping squares ii solution
Solution to the Two Overlapping Squares II Puzzle
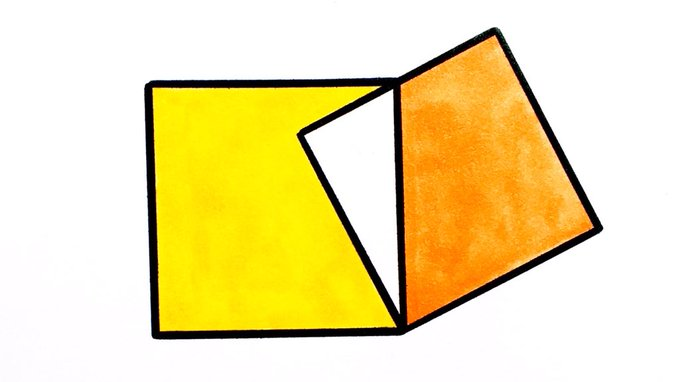
Half the total area of these overlapping squares is yellow. What fraction is orange?
Solution by Similar Triangles, Congruency, Angles in a Square, and Vertically Opposite Angles
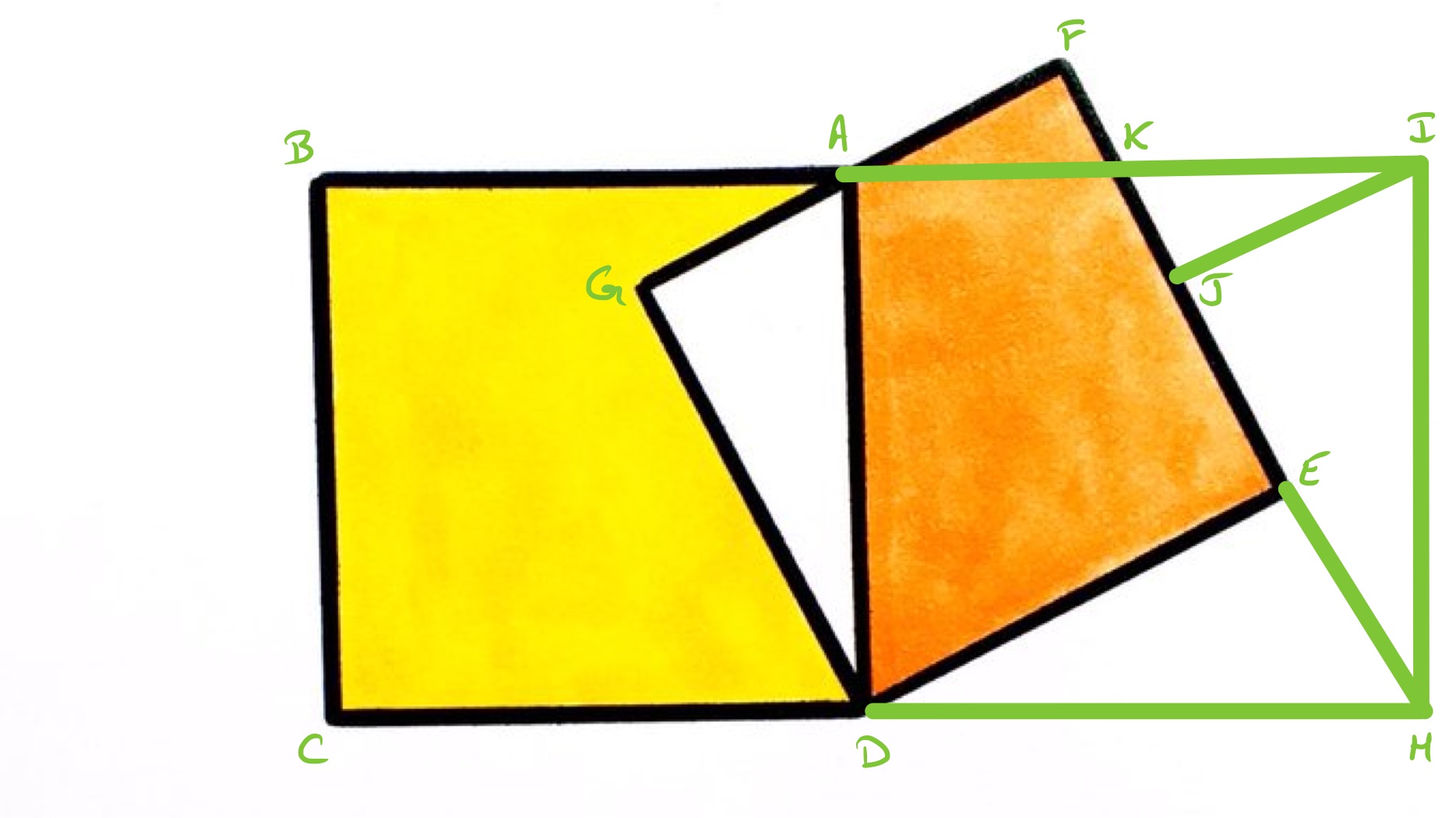
In the extended diagram above, the line is the continuation of until it meets the extension of . The point makes into a rectangle, and is so that is perpendicular to .
Since is a straight line, angle is . Angles and are equal as both combine with angle to form a right-angle, and line segments and have the same length. These establish triangles and as congruent so has the same length as which means that is actually a square and is the congruent to .
Each side of triangles is parallel to one of the sides of triangle and sides and are the same length so triangles and are congruent. This means that the region is congruent to the yellow region.
The yellow region comprises half the area of the original diagram, meaning that the orange and white make up the other half. Since triangles and are congruent, the quadrilateral therefore has the same area as the yellow region, which in turn has the same area as . Therefore, triangles and have the same area. These triangles are similar, since both are right-angled and angles and are equal as they are vertically opposite angles. Therefore they are congruent and in particular, and have the same length. This establishes as the midpoint of .
Triangle therefore is one quarter of the area of the square and so the orange region is of that square, which is itself half the total area. So the area of the orange region is ths of the total area.