Notes
two octagons and two squares solution
Solution to the Two Octagons and Two Squares Puzzle
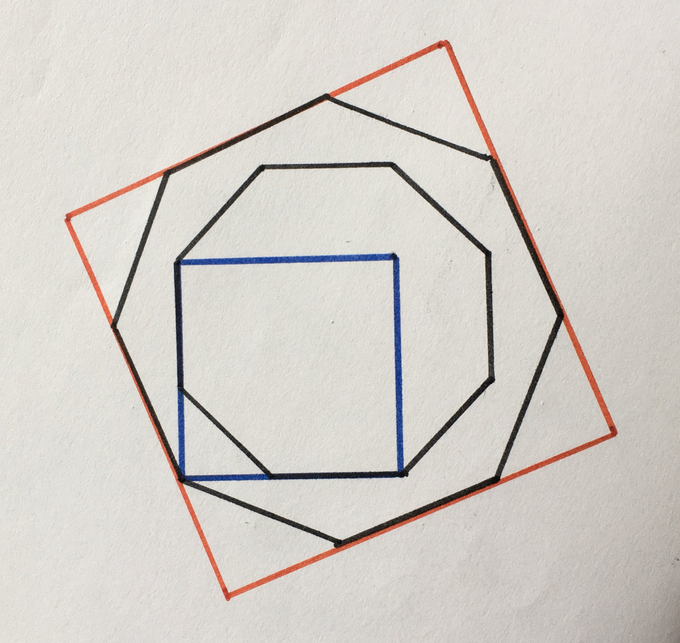
The two regular octagons are concentric. Find [the] relationship between the two squares.
Solution by Pythagoras' Theorem and Lengths in an Isosceles Right-Angled Triangle
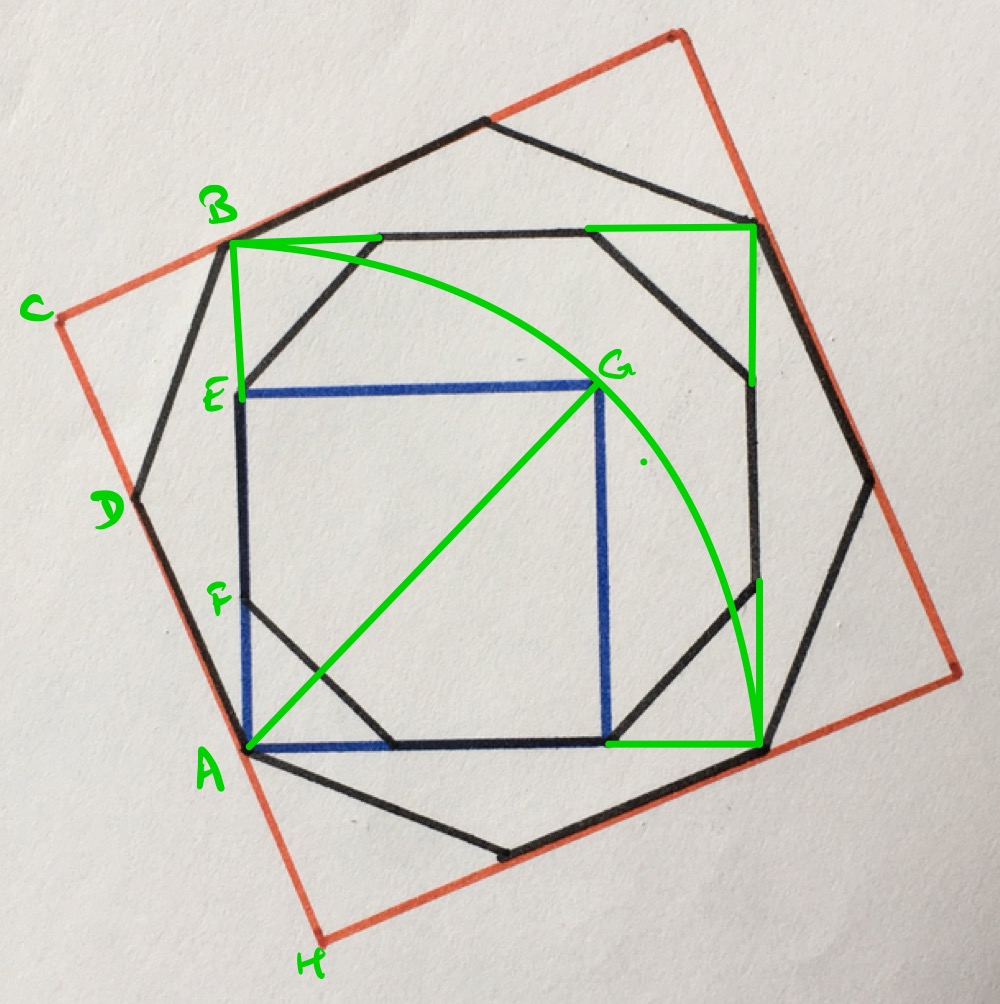
Label the points as in the above diagram. Take the length of line segment as one unit.
Triangle is an isosceles right-angled triangle, so line segment has length . Therefore, line segment has length and the outer square has side length .
Applying Pythagoras' theorem to triangle shows that line segment has length:
Similarly, the length of is times the length of and the length of is times the length of . Therefore, the length of is times the length of , so is:
The ratio of lengths of the sides of the squares is therefore:
In terms of area, the larger square has area times that of the smaller.