Notes
two isosceles triangles solution
Two Isosceles Triangles
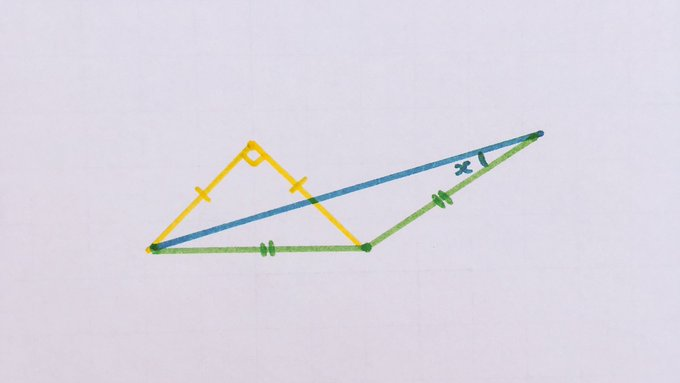
These two isosceles triangles have the same area. What’s the angle?
Solution by Properties of Isosceles Triangles and Equilateral Triangles
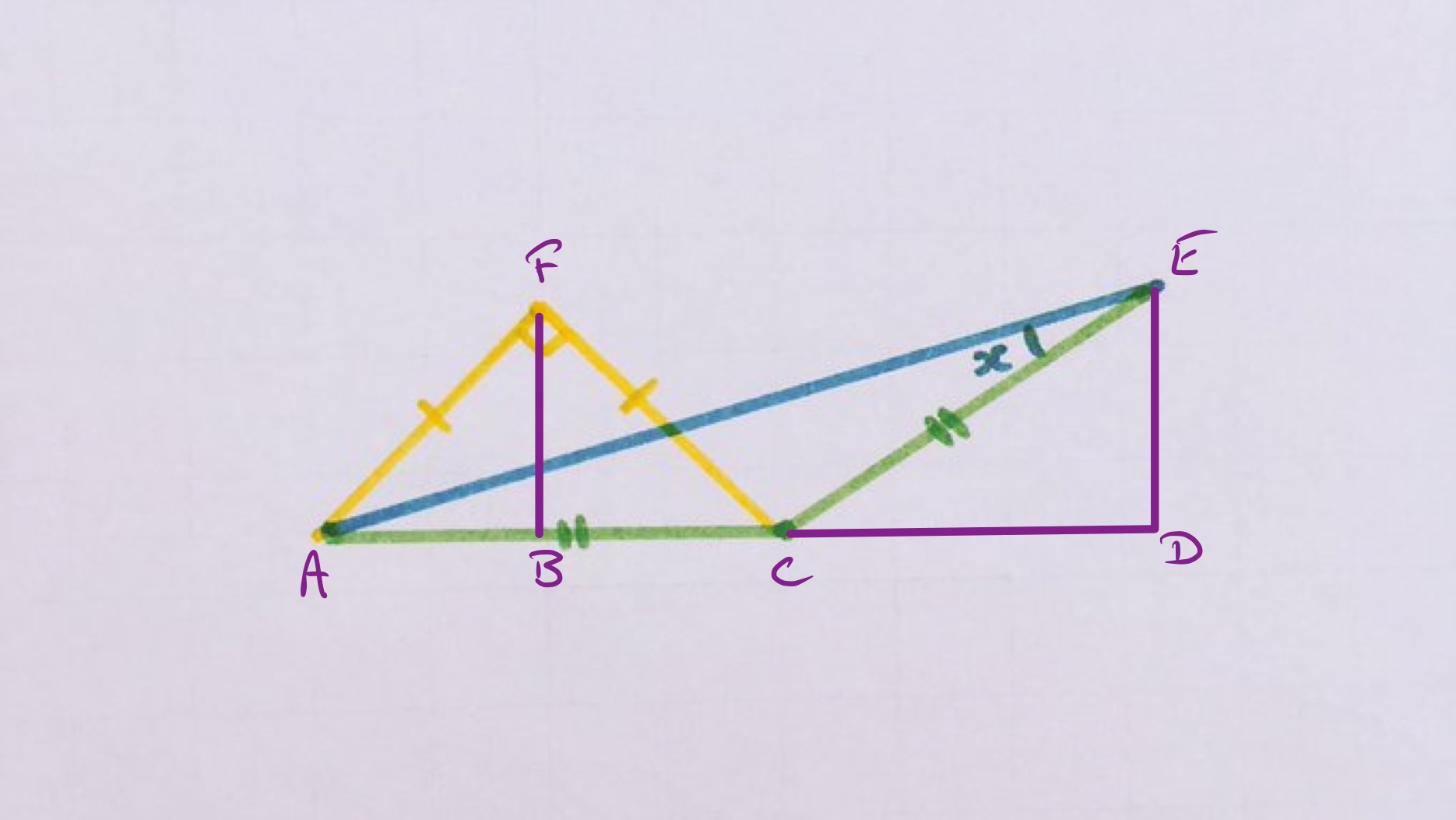
As both isosceles triangles have the same base and area, they must have the same height. So in the above diagram, and have the same length. Since triangle is an isosceles right-angled triangle and is the midpoint of , triangle is also isosceles and right-angled and so the length of is the same as that of and so half of that of . This means that has half the length of , so triangle is half an equilateral triangle. Angle is therefore so angle is , and finally angle is .