Notes
two half-squares and a circle solution
Solution to the Two Half-Squares and a Circle Puzzle
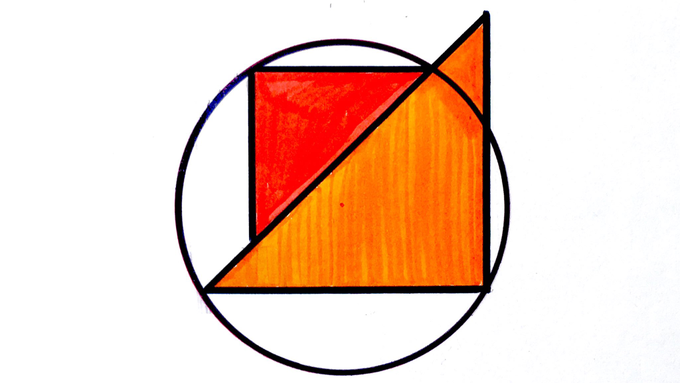
Two half squares, and a circle of radius . What’s the total shaded area?
Solution by Properties of Chords and Pythagoras' Theorem
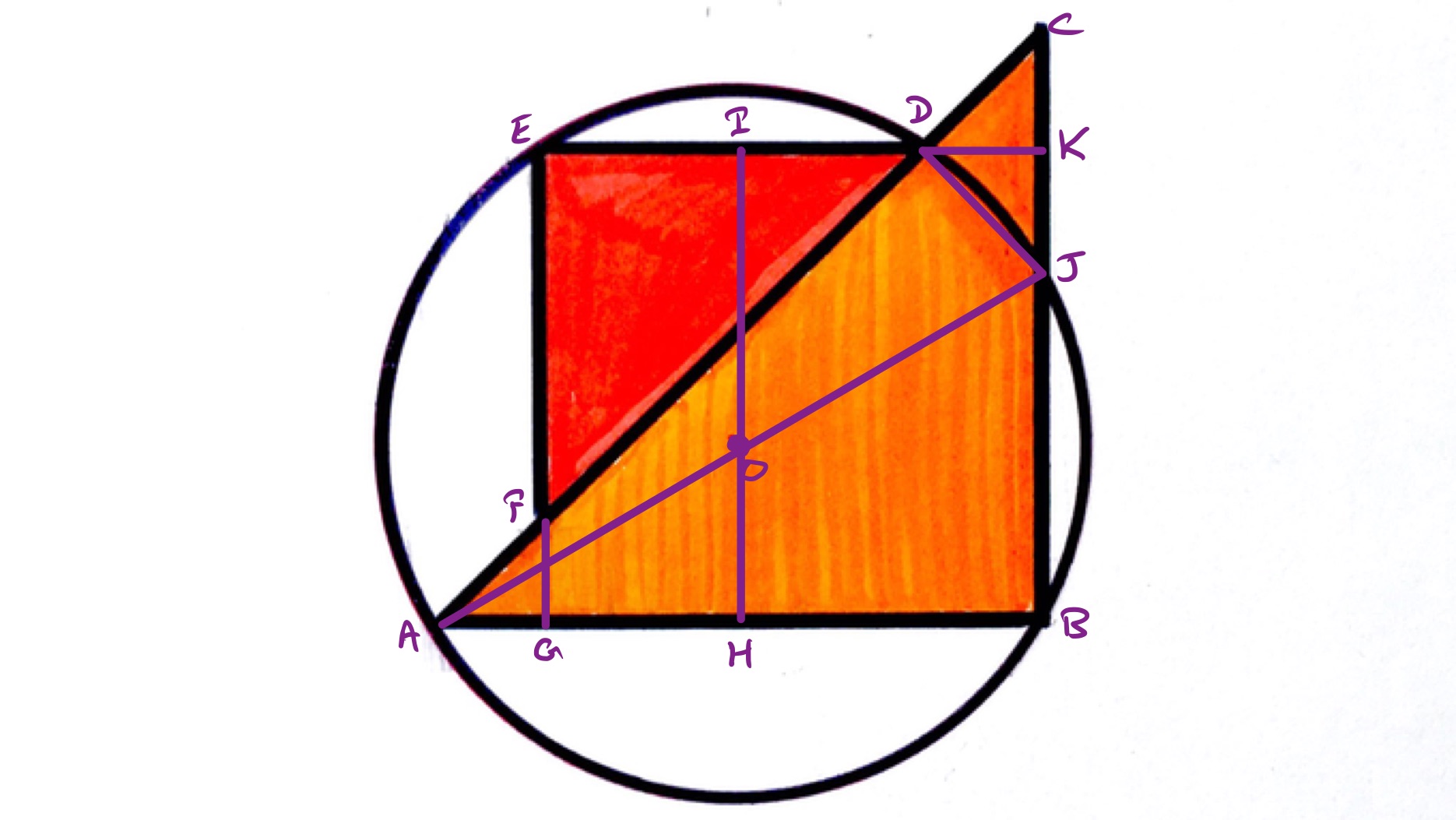
In the above diagram, point is the middle of the circle, is the midpoint of and is the midpoint of . The point is where the extension of meets , and likewise is where the extension of meets .
As is a chord of the circle, the centre of the circle lies on the perpendicular line through its midpoint (namely, ). The same argument applied to shows that the centre also lies on the perpendicular line through . As and are parallel, these perpendicular lines are also parallel. Since the centre lies on both, they must therefore be the same line. So the points , , and lie on a straight line that is perpendicular to both and .
This establishes as lying symmetrically over , and so the excess on one side, which is the length of , is equal to the excess on the other, which is the length of . Since is an isosceles right-angled triangle, has the same length as .
The line is a chord with the property that angle is a right-angle, so as the angle in a semi-circle is a right-angle, must be a diameter. By the same result, angle is also a right-angle, so since angle is , angle is . This means that triangle is also an isosceles right-angled triangle and so also has the same length as .
Then the length of is that of with two lengths of removed. This is the same as the length of .
Let be the length of (and thus of ) and the length of . The shaded region has area . Triangle is a right-angled triangle with hypotenuse and other side lengths and , so by Pythagoras' theorem, . Hence the shaded area is .
Solution by Invariance Principle
There are two special cases of this diagram. One in which both triangles are the same size, and one where one triangle has shrunk to zero size.
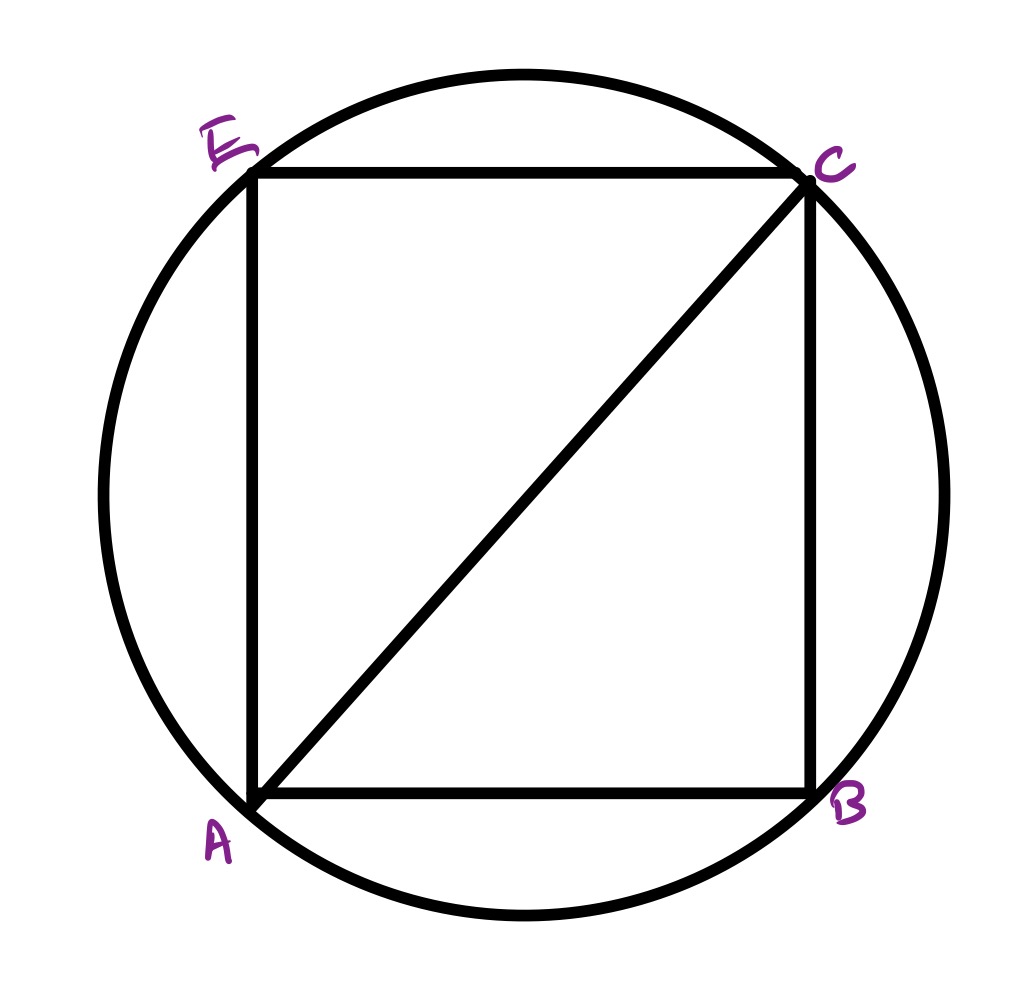
In this version, the total shape makes a square inside the circle. The diagonal of the square coincides with a diameter, since the area of a square is half the square of its diagonal, this establishes the area as .
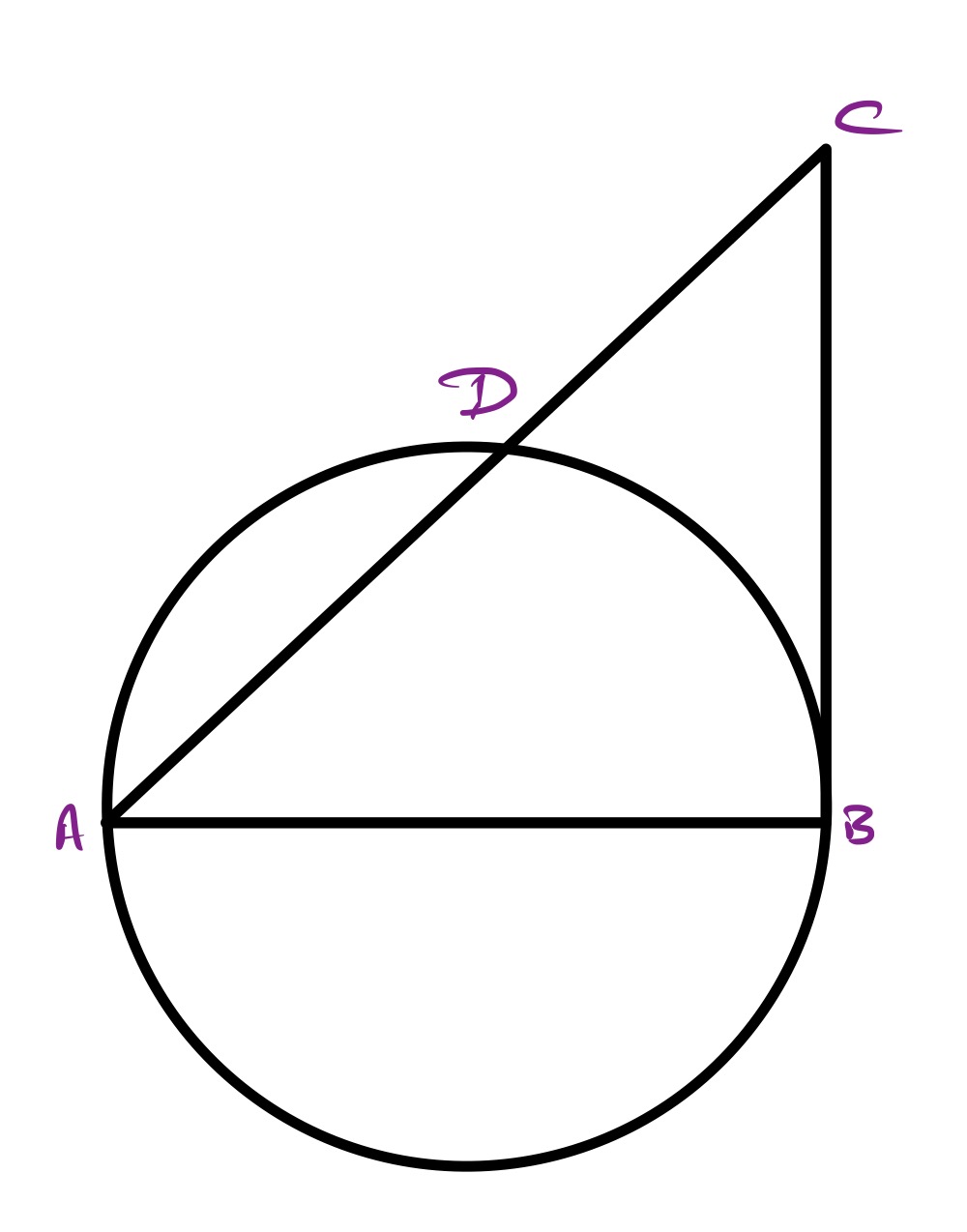
In this version, the total shape is an isosceles right-angled triangle with one side as a diameter of the circle, so the area is .