Notes
two equilateral triangles in a semi-circle solution
Two Equilateral Triangles in a Semi-Circle
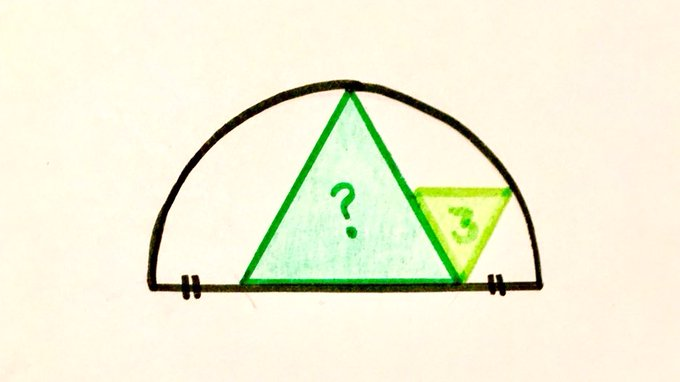
There are two equilateral triangles inside this semicircle. What’s the area of the larger one?
Solution by Symmetry and Properties of Equilateral Triangles
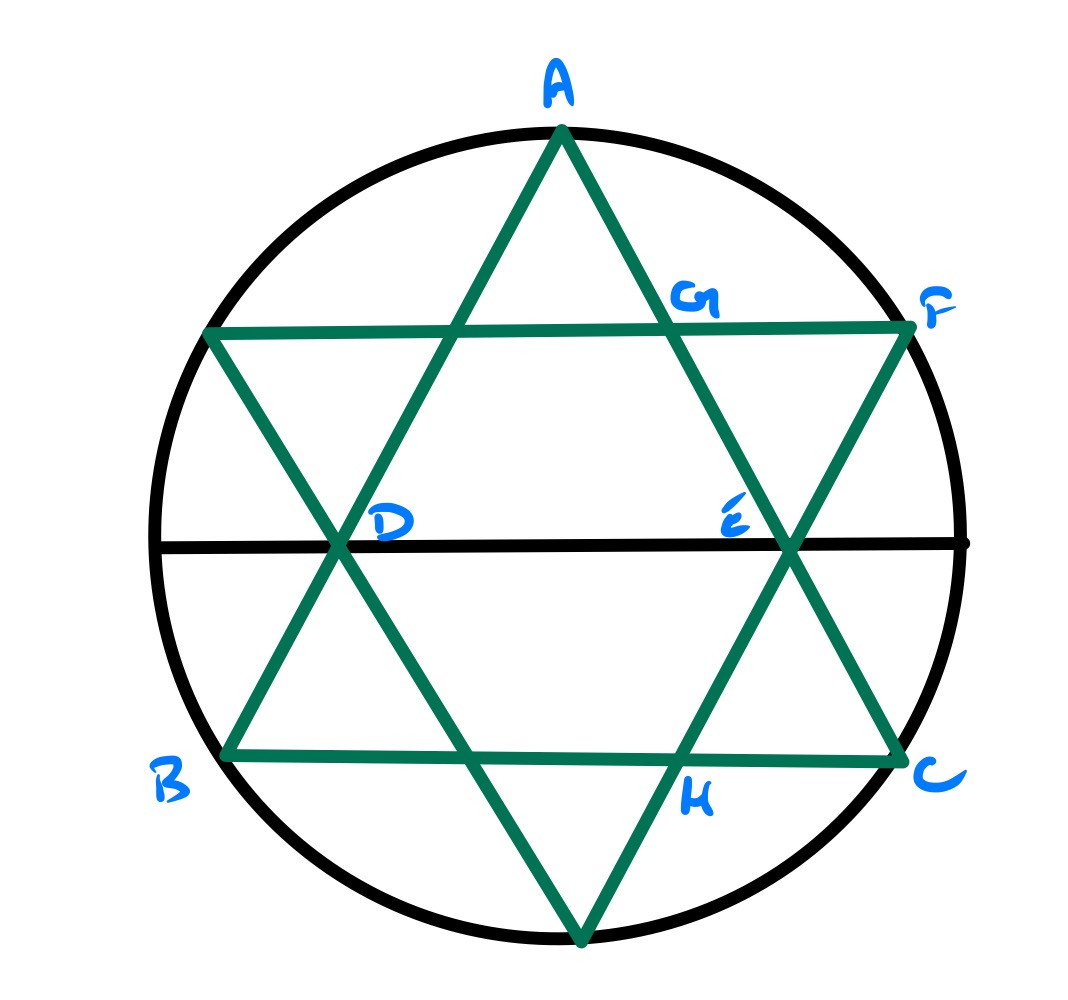
The above diagram consists of reflecting the original one in the base of the semi-circle and adding in the smaller triangles on the left. That is the continuation of comes from filling in all the angles at . Since and are equally spaced on the diagonal, reflection about the central vertical line shows that is an equilateral triangle and the circle is its circumcircle. The height of the centre of the circle above is therefore one third of the height of above , and so is one third of . Since has the same length as , this means that is half of and so the larger of the triangles has four times the area of the smaller. It therefore has area .