Notes
two equilateral triangles iii solution
Solution to the Two Equilateral Triangles III Puzzle
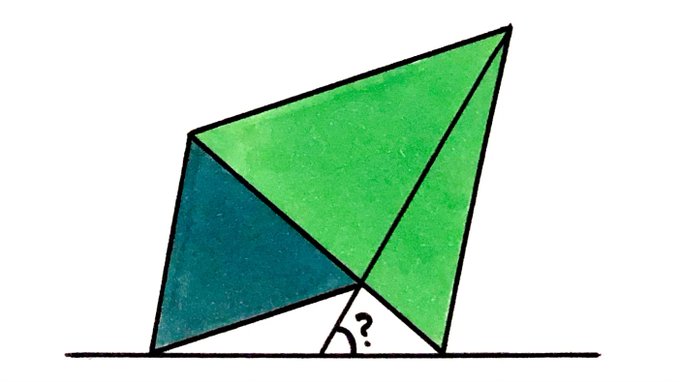
Two equilateral triangles. What’s the angle?
Solution by Properties of Equilateral Triangles, Vertically Opposite Angles, Angles at a Point on a Straight Line, and Congruent Triangles
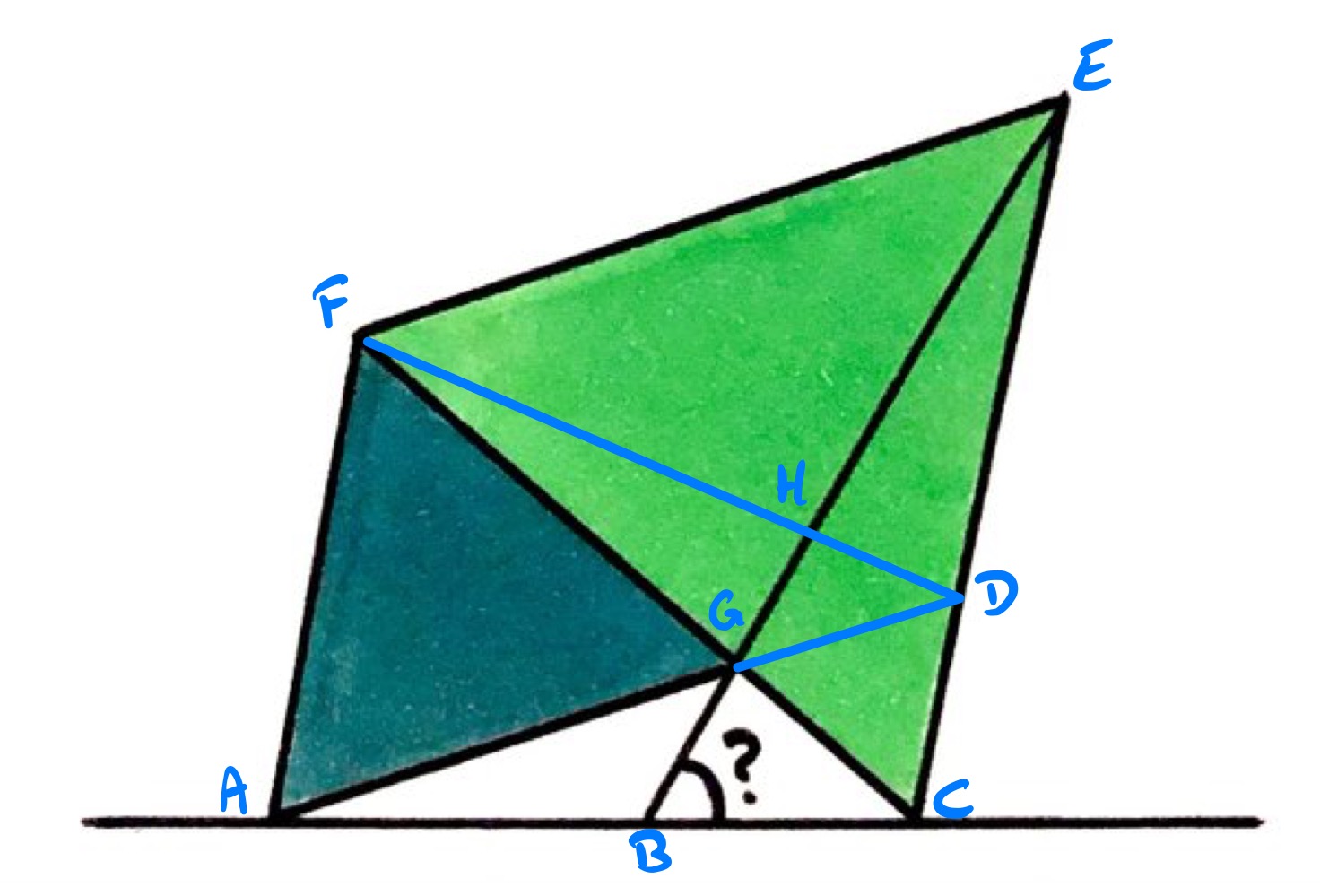
Consider the diagram as labelled above. In this diagram, line segment is the continuation of .
Since vertically opposite angles are equal, angle is the same as angle , hence is . Therefore, two of the angles in triangle are and so triangle is equilateral.
Therefore, line segments and have the same length, so so also do line segments and . Angles and are both , since angles at a point on a straight line add up to , so triangles and are congruent. In particular, angle is the same as angle .
Similarly, line segments and have the same length, as do and . Then also angles and are equal. So triangles and are also congruent. In particular, angles and are equal.
So angle is equal to angle . Moreover, angles and are equal as they are vertically opposite. Therefore, angles and are also equal, but is equal to . So angle is equal to since angles at a point on a straight line add up to .
Solution by Invariance Principle
The relative sizes of the equilateral triangles can vary, leading to the following two configurations.
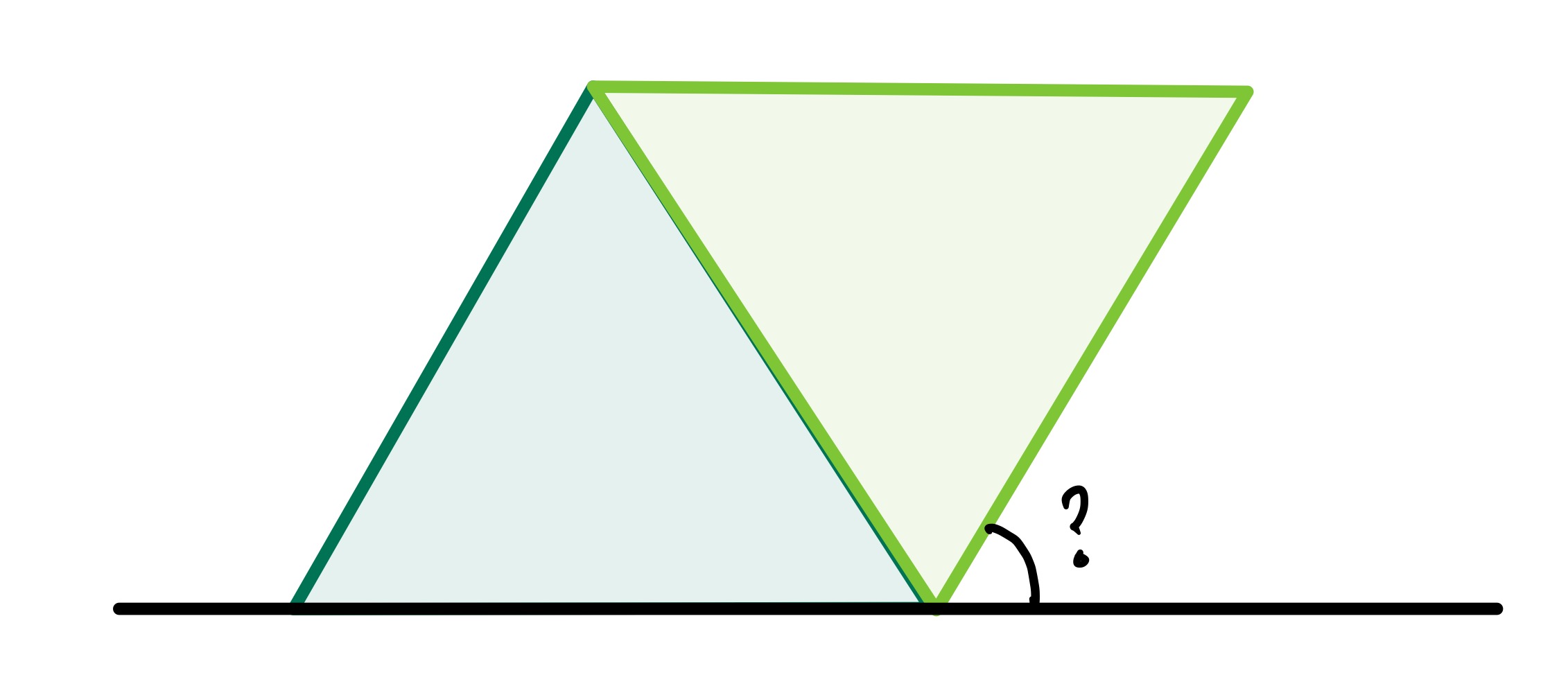
In this version of the diagram, the two equilateral triangles are the same size and the requested angle is then .
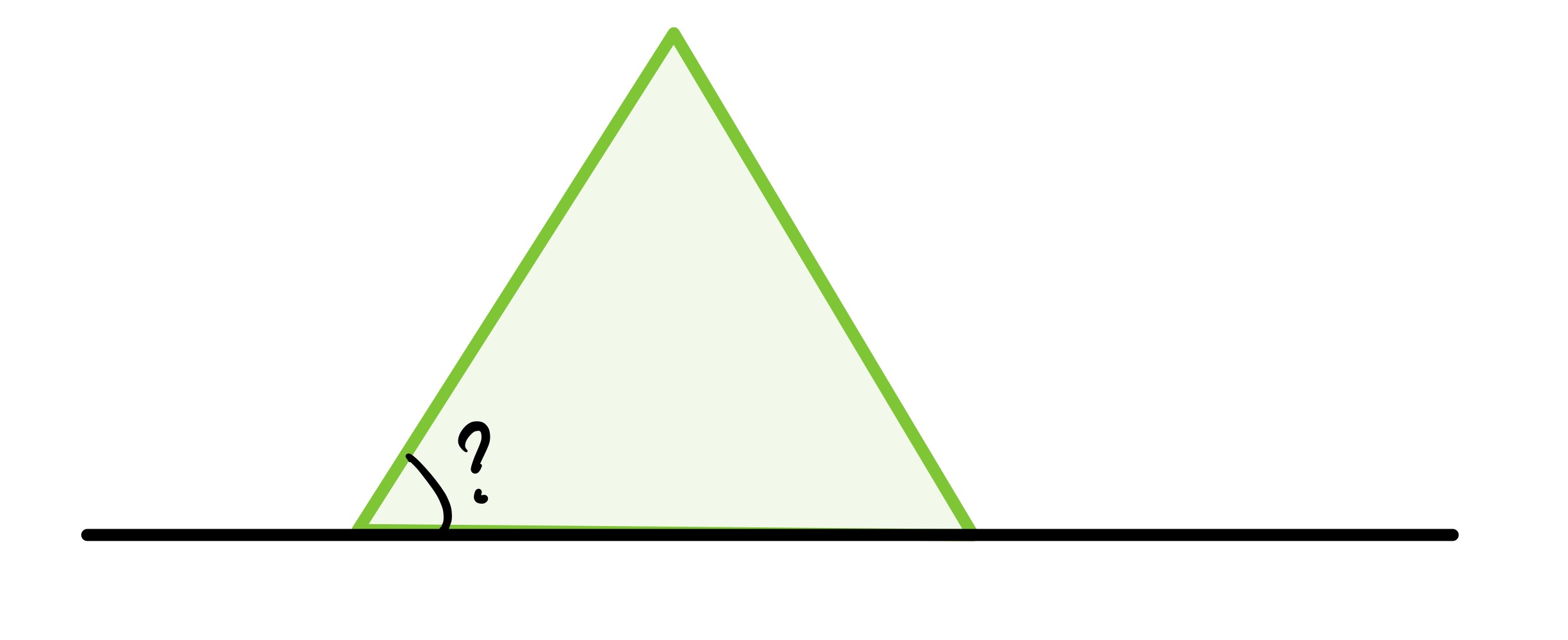
In this version, one triangle has shrunk down to a point and the requested angle is the interior angle of an equilateral triangle, so is .