Notes
two congruent rectangles in a square solution

Two Congruent Rectangles in a Square

Solution by Similar Triangles and a lot of algebra

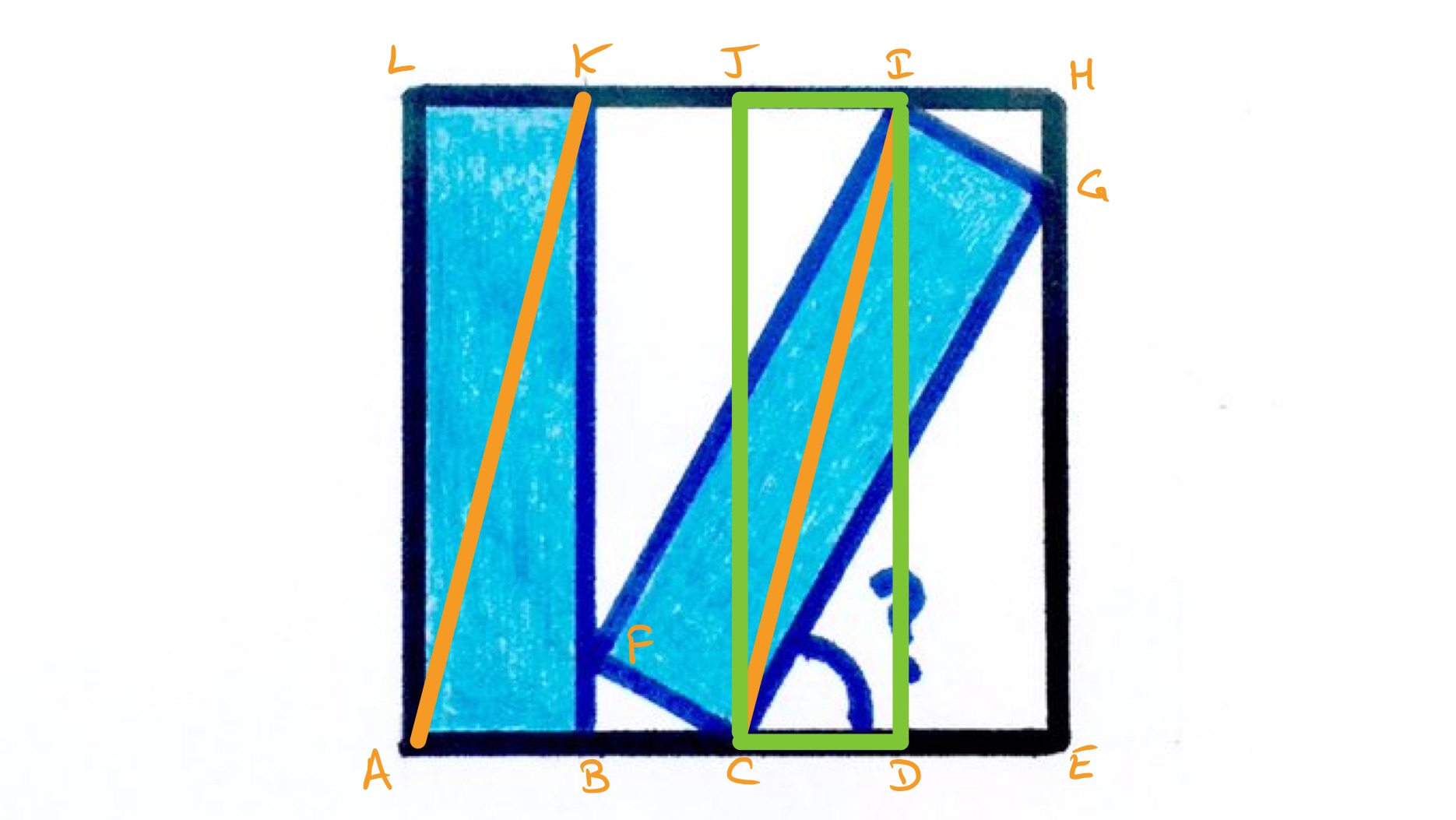
With the points labelled as above, work in units so that the outer square has side length $1$. With this convention, let $a$ be the length of $A B$, $b$ of $C E$, and $c$ of $E G$.

Triangles $C E G$ and $F B C$ are similar, with scale factor $a$, so $B C$ has length $a c$. Also, triangle $G H I$ is congruent to $F B C$ so $H G$ has length $a b$. Therefore, $E H$ has length $c + a b$ and $A E$ has length $a + a c + b$. These are both equal to $1$, so:

Added these together gives $a + (a + 1)(c + b) = 2$, so $c + b = \frac{2 - a}{1 + a}$. Likewise, subtracting gives $c - b = \frac{a}{1 - a}$. So:

Triangle $C E G$ is right-angled, and $C G$ has length $1$, so applying Pythagoras' theorem shows that $b^2 + c^2 = 1$ which leads to:

Either by inspection or by noting that there is a solution where the two rectangles each occupy half the square, this equation can be seen to have a root at $a = \frac{1}{2}$. Dividing out by $1 - 2 a$ results in the quadratic:

which has roots $2 \pm \sqrt{3}$. As $2 + \sqrt{3}$ is greater than $1$, the solution must be $2 - \sqrt{3}$. Substituting in for $b$ gives $b = \frac{1}{2}$. This means that $C E$ is half the length of $C G$, and so triangle $C E G$ is half an equilateral triangle so angle $E \hat{C} G$ is $60^\circ$.

Solution by Lengths in Rectangles and Equilateral Triangles

With the points labelled as in the diagram above, $C I$ is a diagonal of the blue rectangle so is the same length as $A K$. The quadrilateral $A C I K$ therefore has two sides the same length ($A K$ and $C I$) and the other two sides parallel. It is therefore a parallelogram and in particular $C I$ is parallel to $A K$.

This means that reflecting rectangle $F C G I$ in $C I$ produces the rectangle $C D I J$ with $C D$ along $A E$ and $I J$ along $H L$. So this is a horizontal translate of rectangle $A B K L$. In particular, $C D$ has the same length as $A B$ and $D$ is directly below $I$.

Triangles $F B C$ and $G H I$ are congruent, so $B C$ and $I H$ have the same length, and so $B C$ and $D E$ have the same length. This means that $A C$ and $C E$ have the same length, so $C E$ is half the length of $A E$ and thus half the length of $C G$.

As above, this means that $G C E$ is half an equilateral triangle so angle $E \hat{C} G$ is $60^\circ$.