Notes
two congruent rectangles and a semi-circle solution
Solution to the Two Congruent Rectangles and a Semi-Circle Puzzle
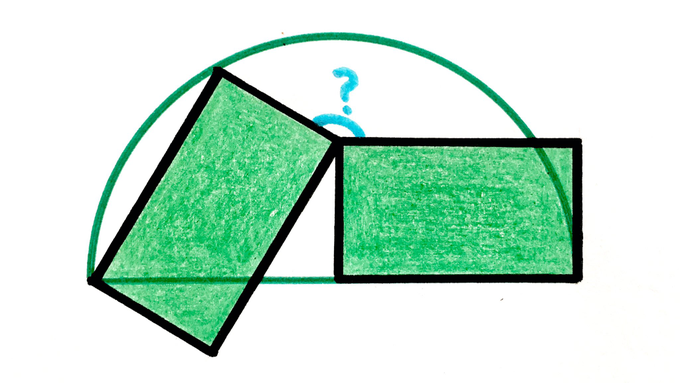
The two rectangles are congruent. What’s the angle?
Solution by Congruent Polygons and Angles of Triangles
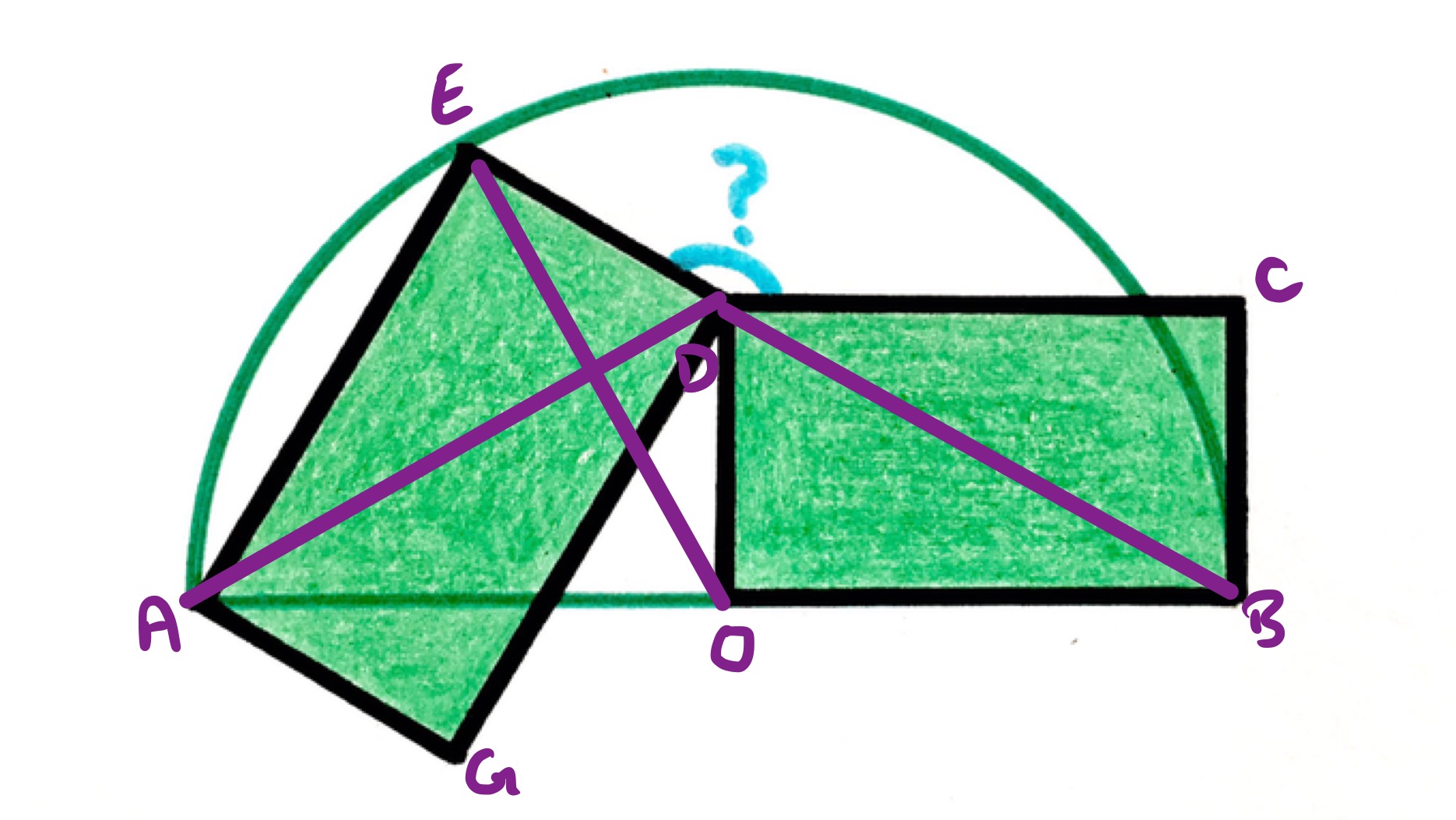
The goal is to show that in the above diagram then point is the centre of the semi-circle. As the rectangles are congruent, their diagonals are the same length and so the lengths of and are the same. Triangles and are both right-angled triangles with two sides the same length. They are therefore congruent and so the lengths of and are the same (this can also be deduced from Pythagoras' theorem). This establishes as the midpoint of the diameter and so as the centre of the circle.
Since is the centre, has the same length as . As this is also the same length as and the rectangles are congruent, the line segment has the same length as and . Triangle is therefore equilateral and so angle is . Angle is then . As the rectangles are congruent, sides and have the same length, and so triangle is isosceles. This establishes angle as also and so since angles in a triangle add up to . Finally, angle since angles at a point add up to .