Notes
two circles solution
Solution to the Two Circles Puzzle
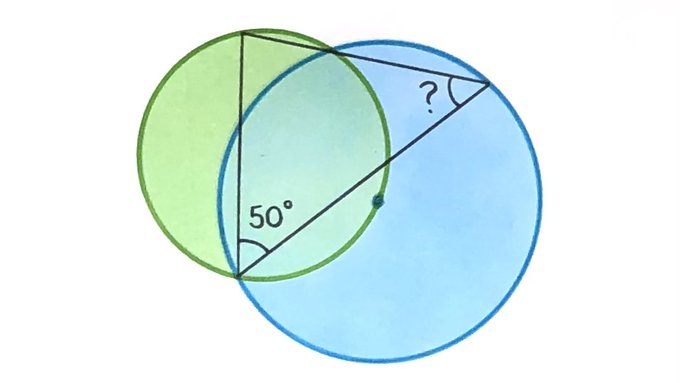
What’s the angle?
Solution by Angles in the Same Segment, Opposite Angles in a Cyclic Quadrilateral, and Angle at the Centre is Twice the Angle at the Circumference
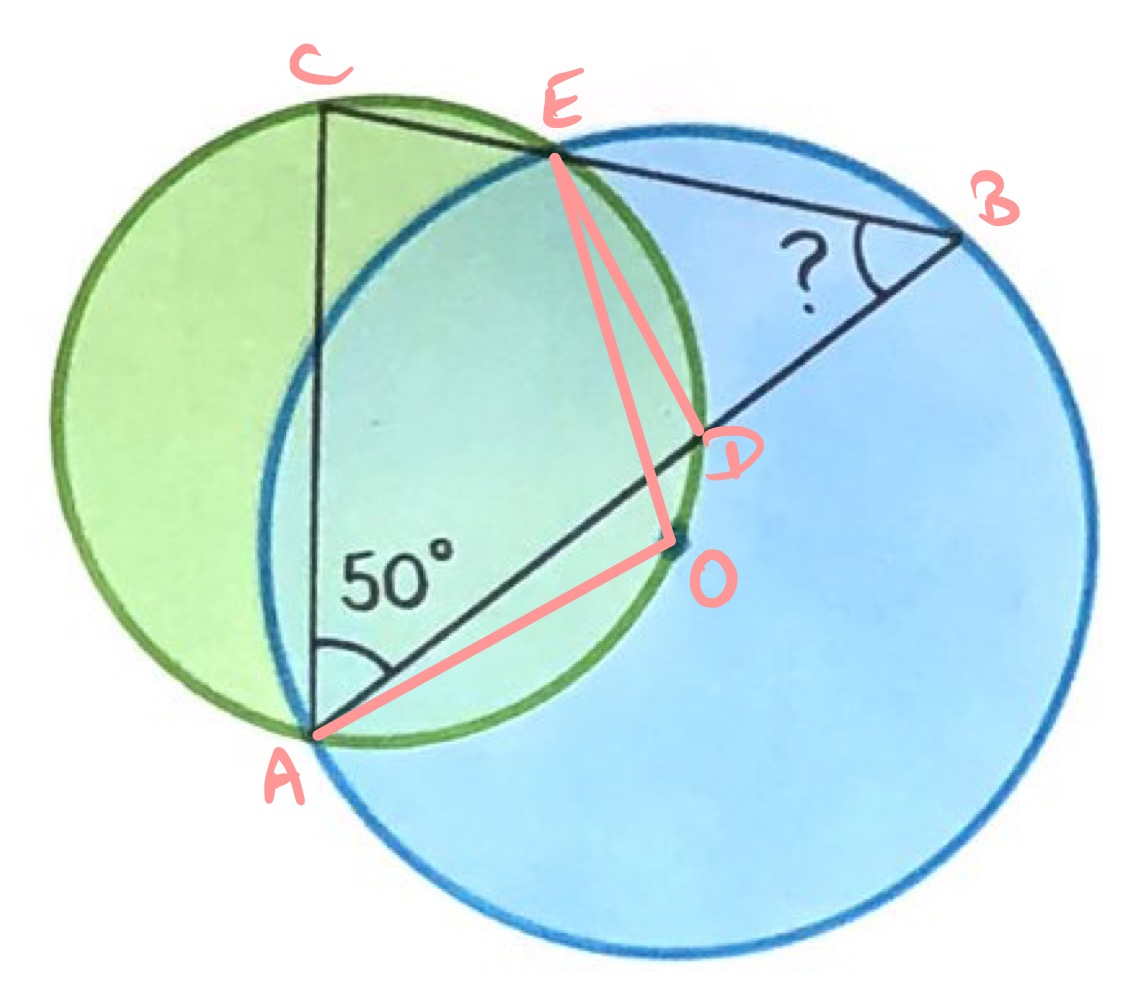
Label the points as above, with the centre of the blue circle.
Angles and are equal since they are angles in the same segment. Then is a cyclic quadrilateral so angles and add up to . But also angles , , and add up to since they are angles in a triangle. Therefore, angles and add up to angle .
Then angle is twice angle since the angle at the centre is twice the angle at the circumference. Hence angles and add up to twice angle , so they must be equal. Thus angle is .