Notes
two circles inside two polygons inside a circle solution
Solution to the Two Circles Inside Two Polygons Inside a Circle Puzzle
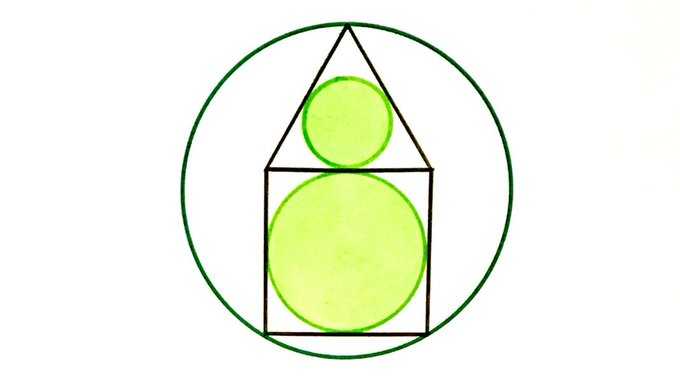
Two circles, inside two regular polygons, inside a large circle. What fraction is shaded?
Solution by Lengths in Equilateral Triangles, Properties of Chords, and Intersecting Chords Theorem
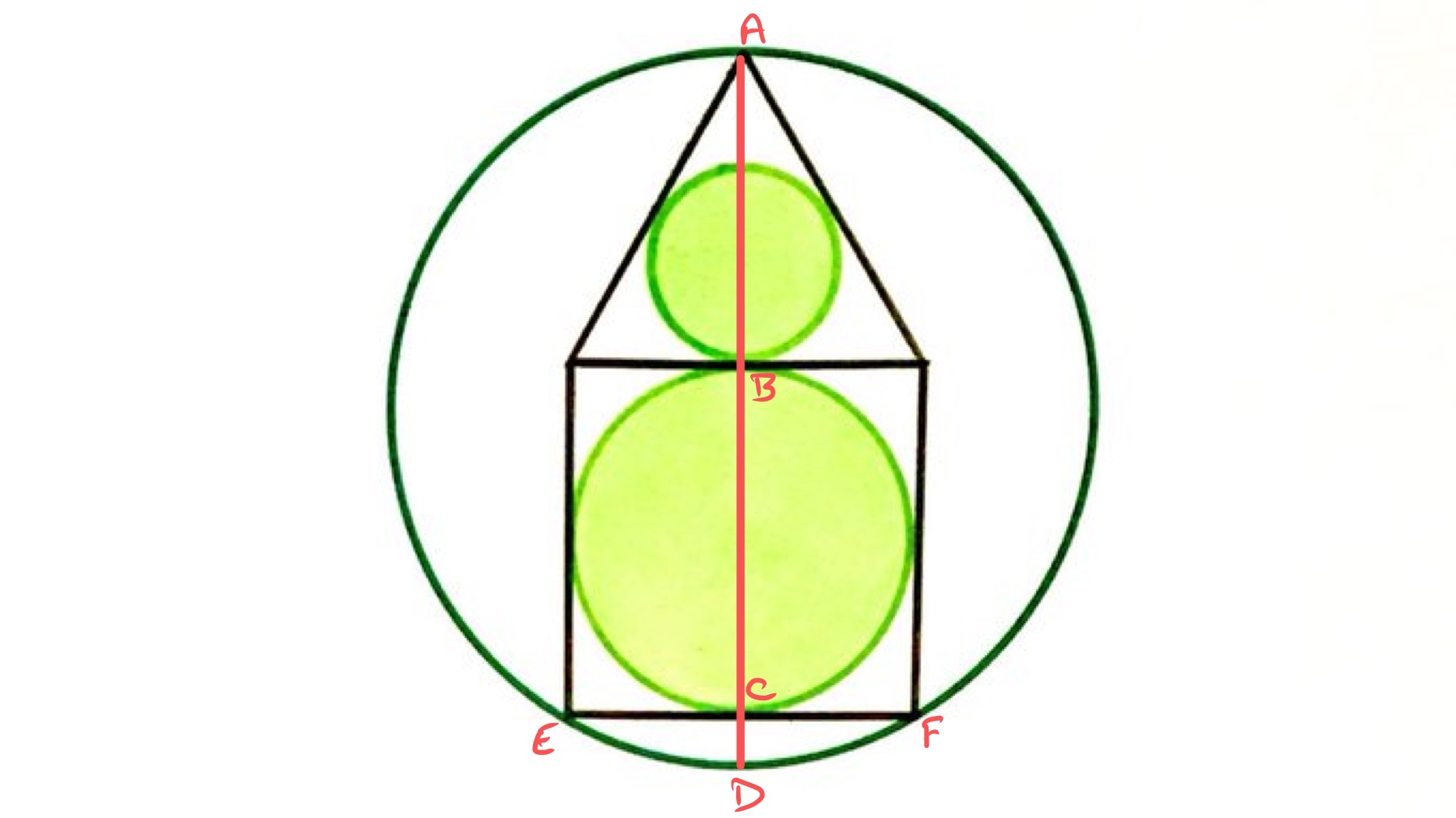
As the line segment is a chord, its perpendicular bisector passes through the centre of the circle and so is a diameter.
Let be the length of half the side of the square, so is the length of . Using lengths in an equilateral triangle, the length of is so the length of is . Write for the length of , then using the intersecting chords theorem applied to and , the and satisfy:
which rearranges to
The diameter of the outer circle is therefore:
Its area is therefore .
The radius of the circle in the square is , and the radius of the circle in the equilateral triangle is a third of the length of , so is . The area of the shaded regions is therefore .
Therefore rd of the outer circle is shaded.