Notes
two circles inside an equilateral triangle solution
Solution to the Two Circles Inside an Equilateral Triangle Puzzle
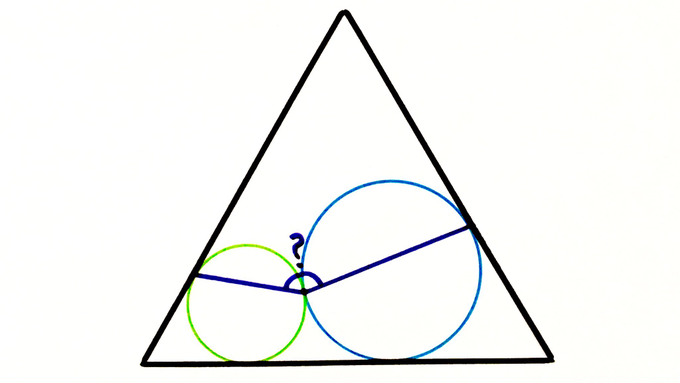
The triangle is equilateral. What’s the angle?
Solution by Isosceles Triangle and Angles in a Quadrilateral
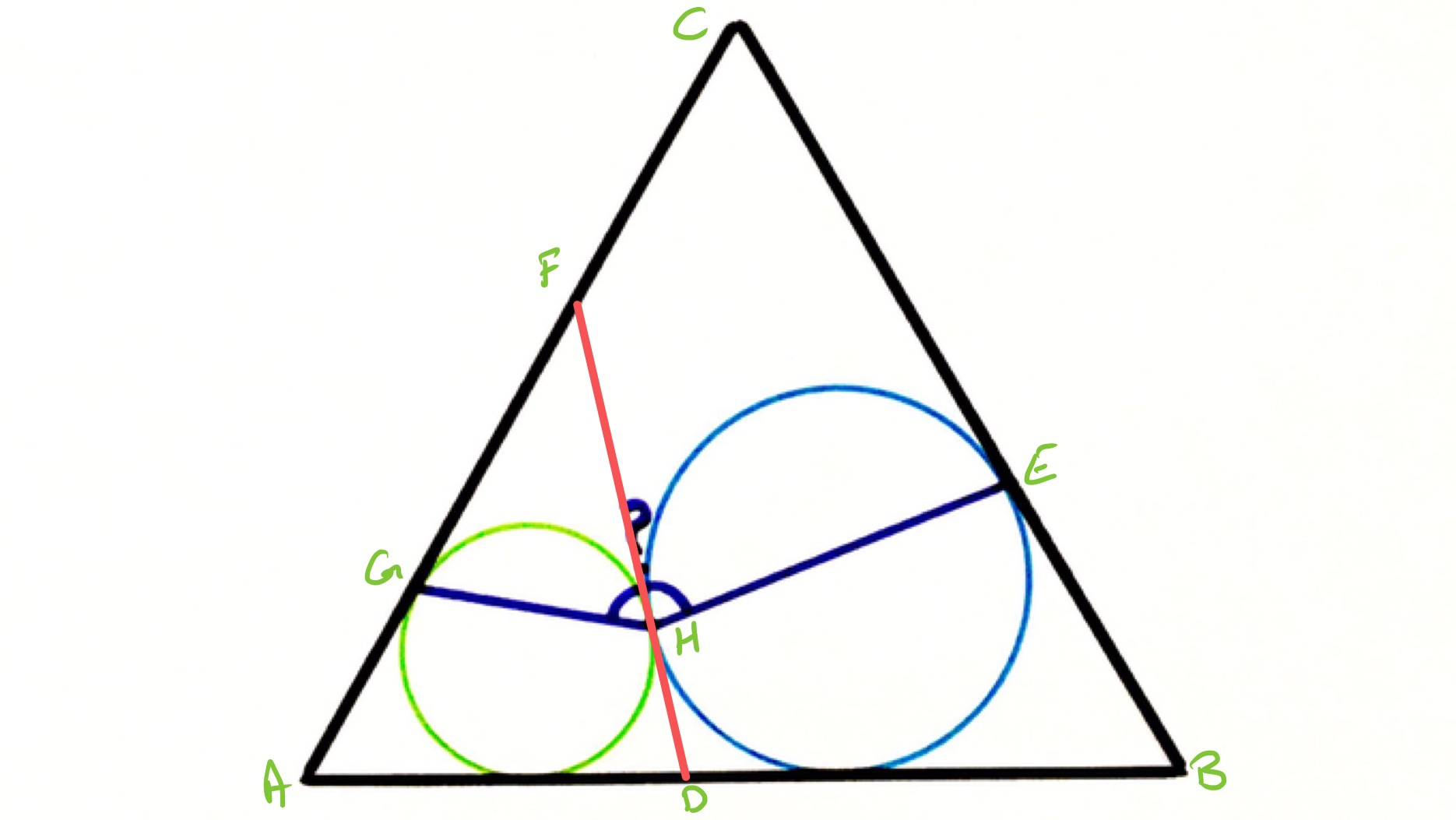
In the above diagram, the line segment is tangent to the two circles at . The lengths of and are the same, so triangle is isosceles and so angles and are equal. Extending and to the point where they meet creates another isosceles triangle to show that angles and are also equal. The sum of the four angles , , , and is then twice the marked angle. As the outer triangle is equilateral, angle is . As the angles in a quadrilateral sum to , this means that angles , , and sum to meaning that the marked angle is .
Solution by Invariance Principle
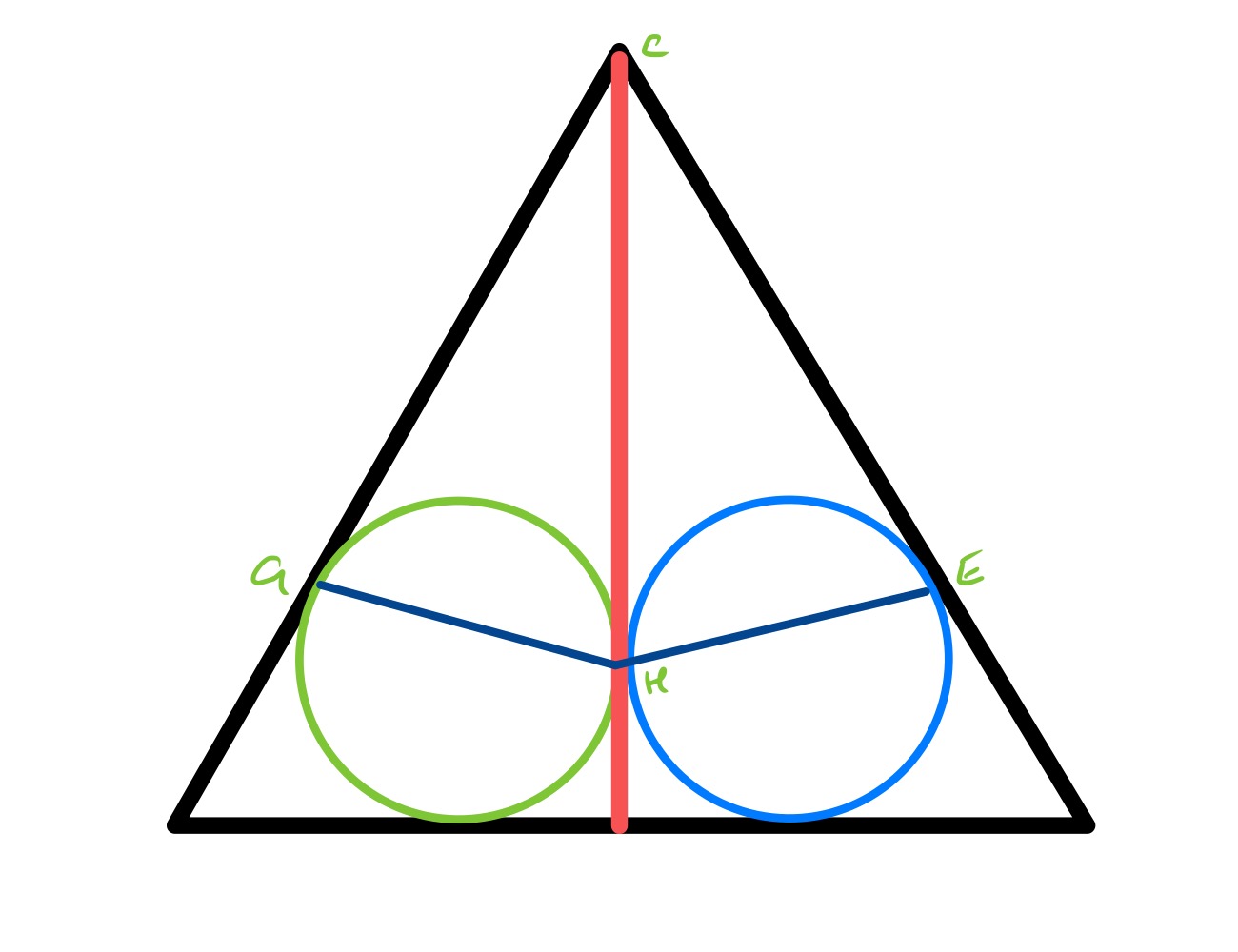
In the above diagram, the two circles are the same size as each other. The red line is then vertical and goes through point . Angles and are both and triangles and are isosceles (and congruent) with base angles half of . So angle is .