Notes
two circles inside a square solution
Two Circles Inside a Square
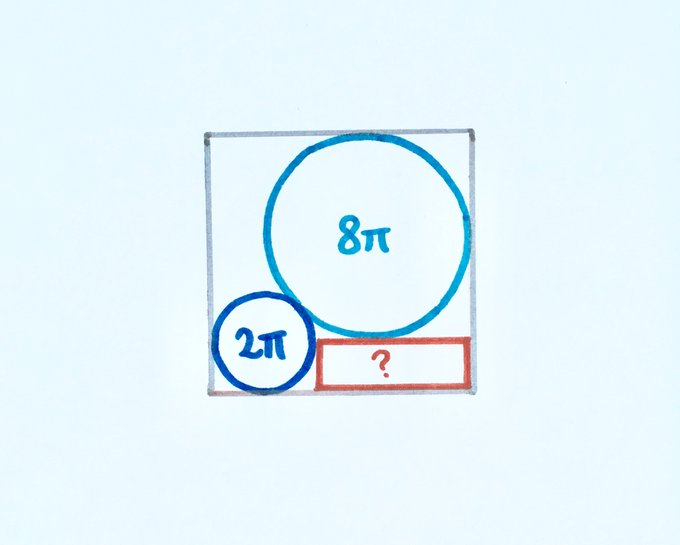
Given the areas of the two circles inside this square, can you find the area of the rectangle?
Solution by Lengths in a Square
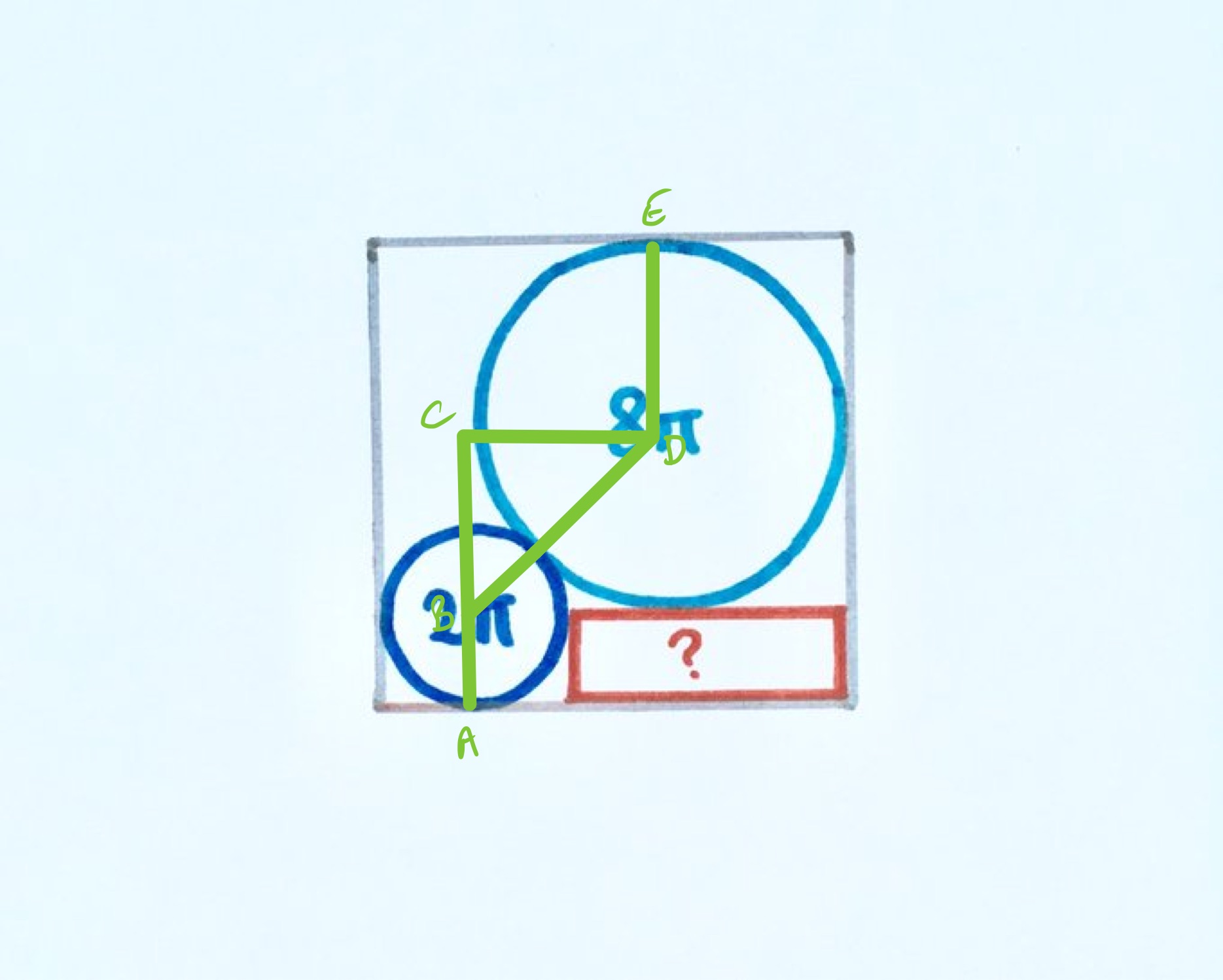
With the points labelled as above, let be the radius of the smaller circle, of the larger, and let be the side length of the square. The unknown rectangle has sides and . The radii satisfy and so and .
Triangle is an isosceles right-angled triangle since the centres of the circles lie on the diagonal of the square. The hypotenuse has length , so the length of is using the relationships between lengths in a square. The side length of the square is then .
The sides of the red rectangle are therefore:
The area of this rectangle is therefore:
Since and , and so . This then simplifies to .