Notes
two circles in a triangle ii solution

Solution to the Two Circles in a Triangle II Puzzle

Solution by Lengths in an Equilateral Triangle

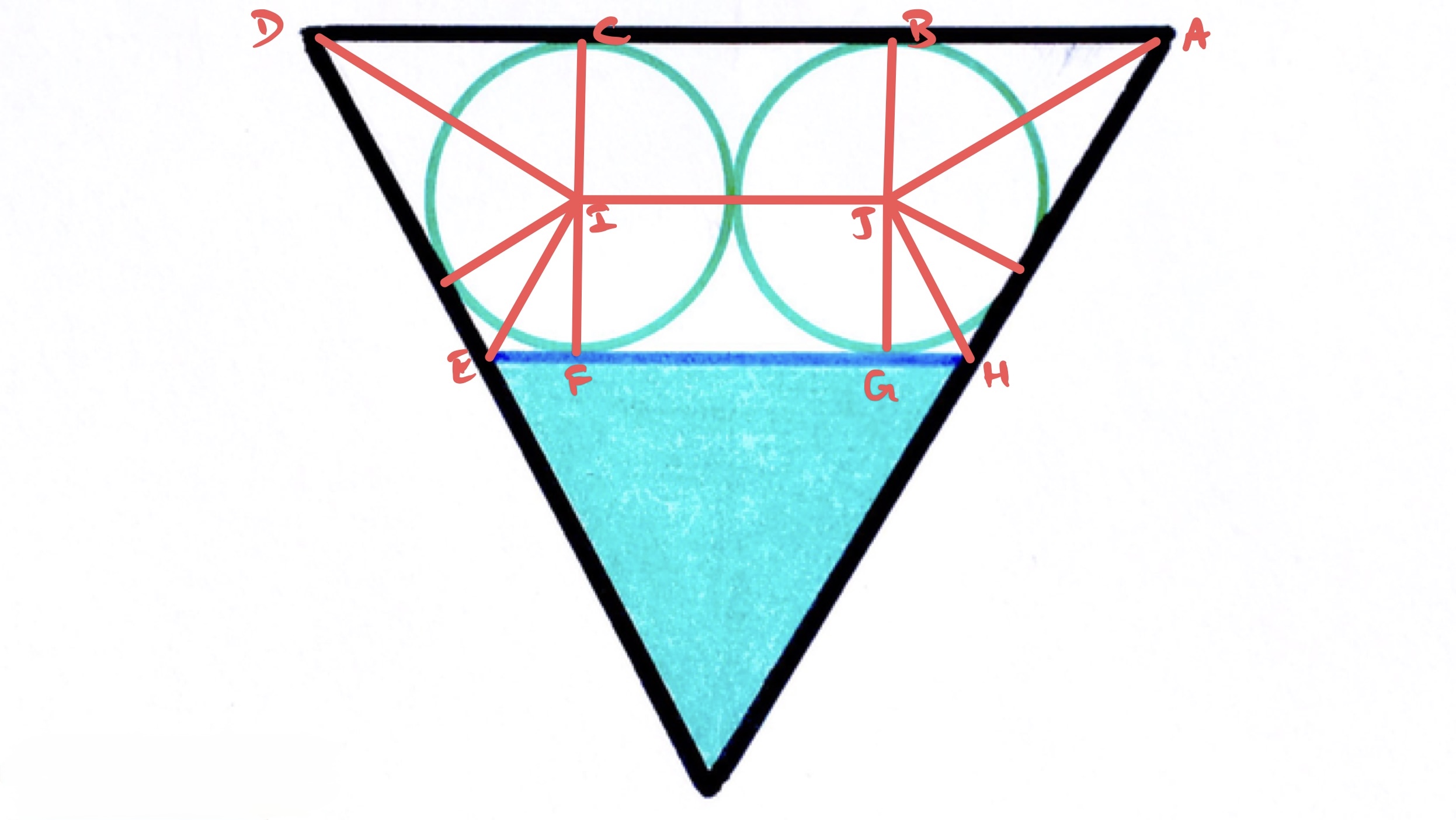
Consider the diagram labelled as above. As the question is one of proportion, it can be assumed that the radius of the circles is $1$. Then $I J$ has length $2$, as do $C B$ and $F G$.

Triangle $D I C$ is half of an equilateral triangle, so the length of $D C$ is $\sqrt{3}$ times that of $C I$, so is $\sqrt{3}$. Therefore, $A D$ has length $2 + 2 \sqrt{3}$.

Similarly, triangle $I E F$ is half of an equilateral triangle, so $I F$ has length $\sqrt{3}$ times that of $E F$, and so $E F$ has length $\frac{1}{\sqrt{3}}$. This means that $E H$ has length $2 + \frac{2}{\sqrt{3}}$.

The length scale factor from the outer triangle to the shaded triangle is therefore:

So the area scale factor is $\frac{1}{3}$ and hence one third of the triangle is shaded.