Notes
two circles in a square solution
Solution to the Two Circles in a Square Puzzle
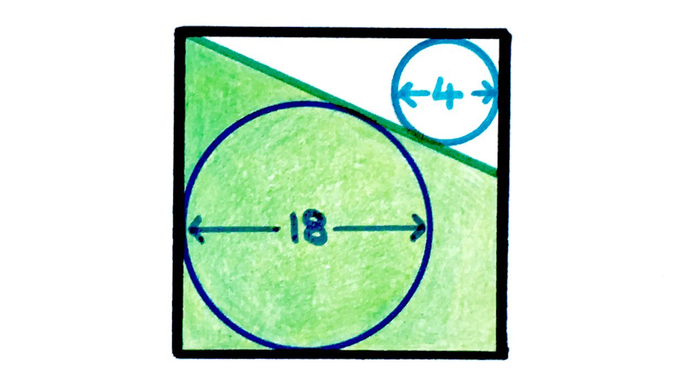
What fraction of the square is shaded?
Solution by Similar Triangles and Angles in Parallel Lines
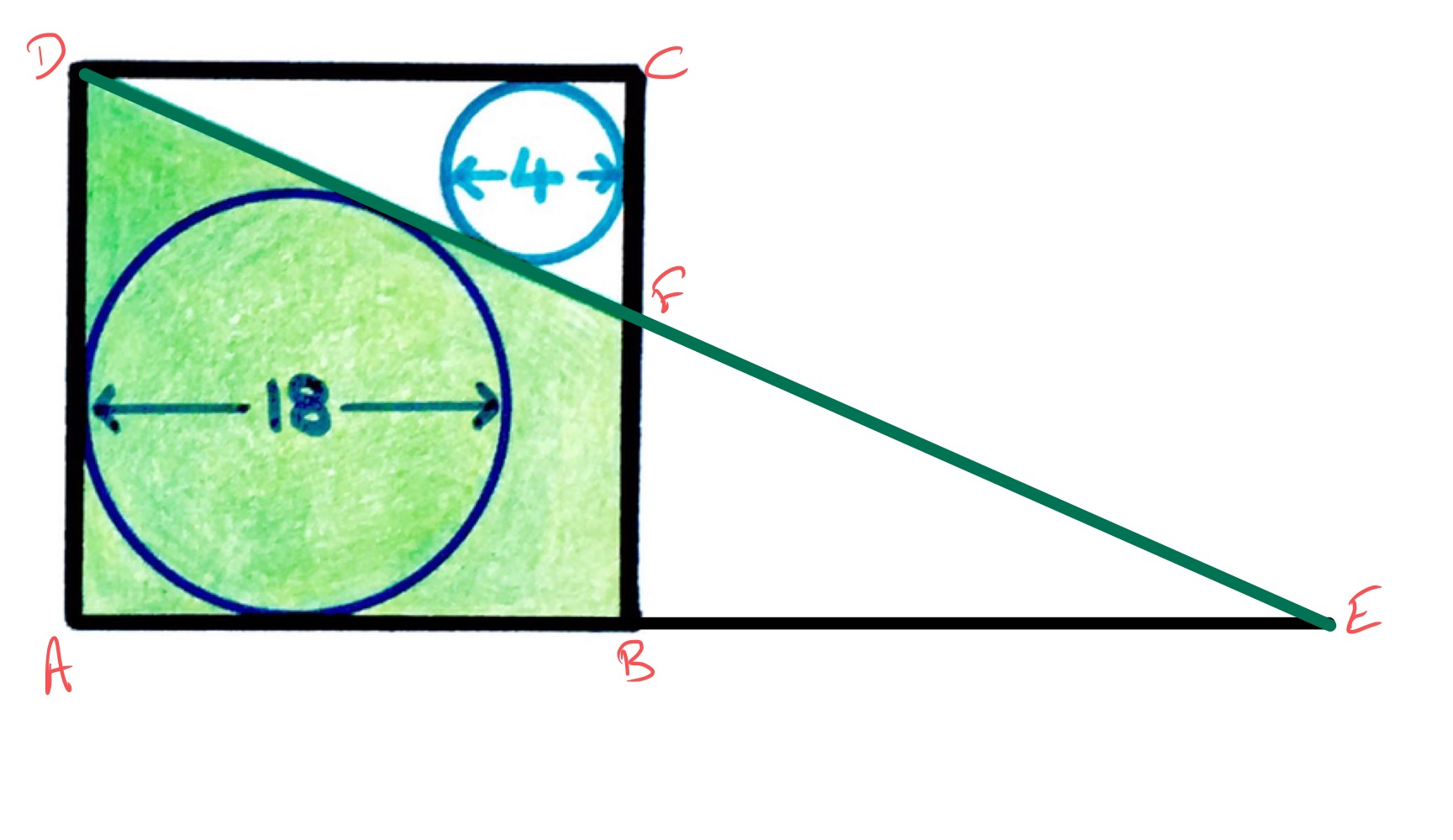
There are three similar triangles in the above diagram: and are similar as they are both right-angled triangles that share the angle . Then is also a right-angled triangle and angle is equal to angle as they are alternate angles.
The circles give the scale factor from triangle to as , meaning that the length of is times the length of .
The area of triangle is half the length of times the length of . The area of the square is the length of times the length of . Therefore the ratio of their areas is the ratio of half the length of to the full length of , which is . So the fraction that is shaded is .