Notes
two circles in a rectangle solution
Two Circles in a Rectangle
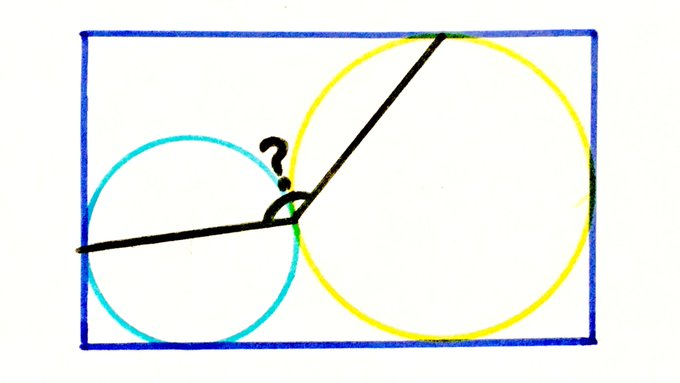
What’s the angle?
Solution by Angle Between a Radius and Tangent, Isosceles Triangle, and Angles in a Quadrilateral
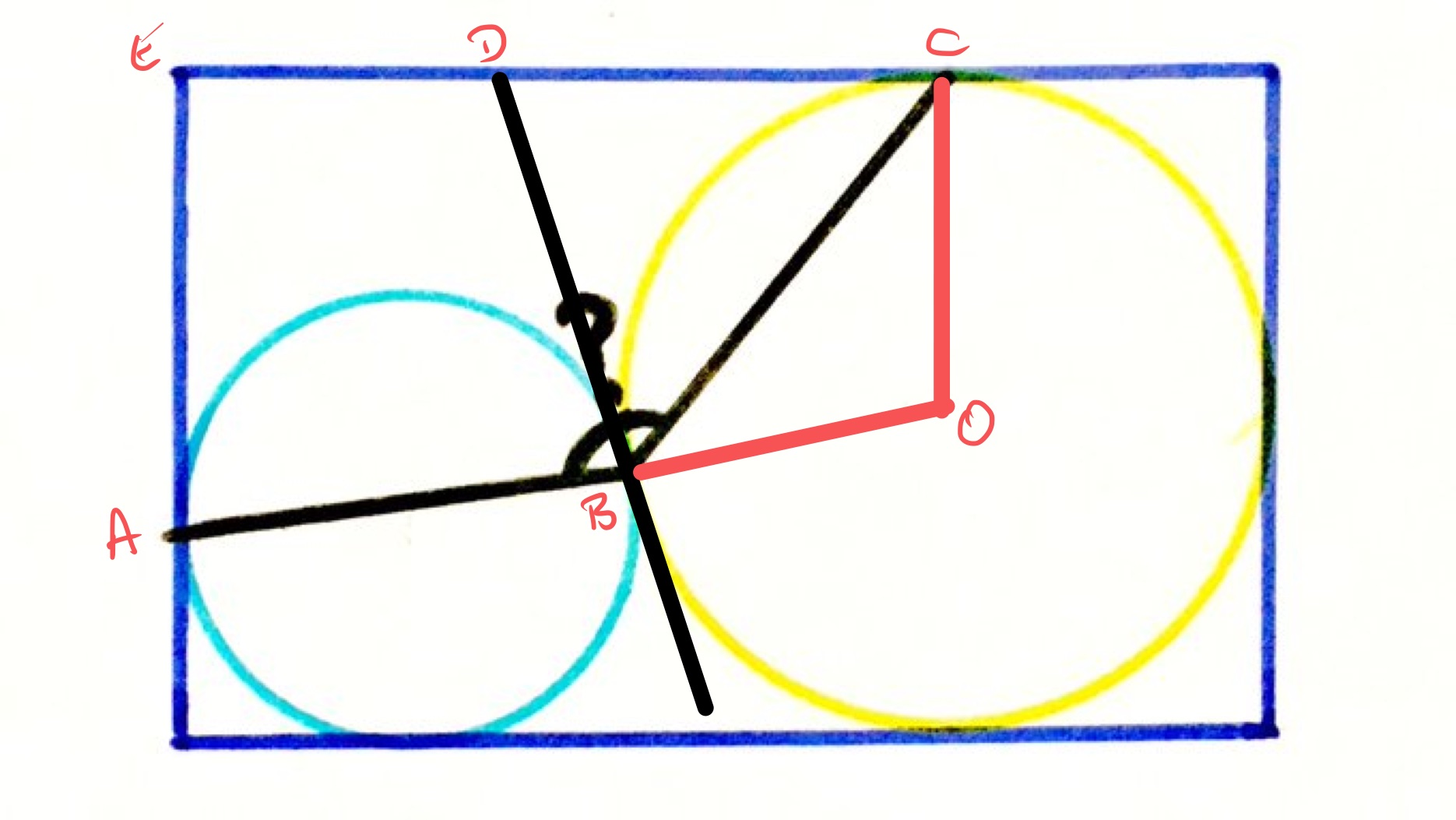
With the points labelled as above, point is the centre of the yellow circle.
Angle is the angle between a radius and tangent so is , as is angle . Since triangle has two radii of the yellow circle, it is isosceles and so angles and are equal. Therefore, angles and are equal. (This can also be seen by considering how the diagram behaves under a reflection through the line through .)
A similar argument shows that angles and are equal. Therefore, the sum of angles and is the same as angle .
Adding up the angles in the quadrilateral , therefore, gives plus twice angle . Since the angles in a quadrilateral add up to , angle must be .