Notes
two circles, two squares solution
Two Circles, Two Squares
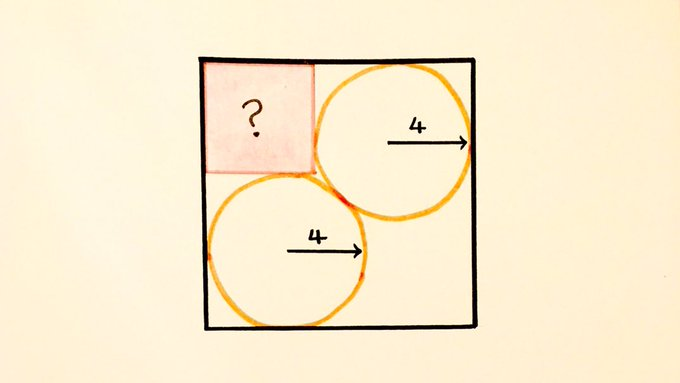
Two circles, two squares. What’s the shaded area?
Solution by Properties of Squares
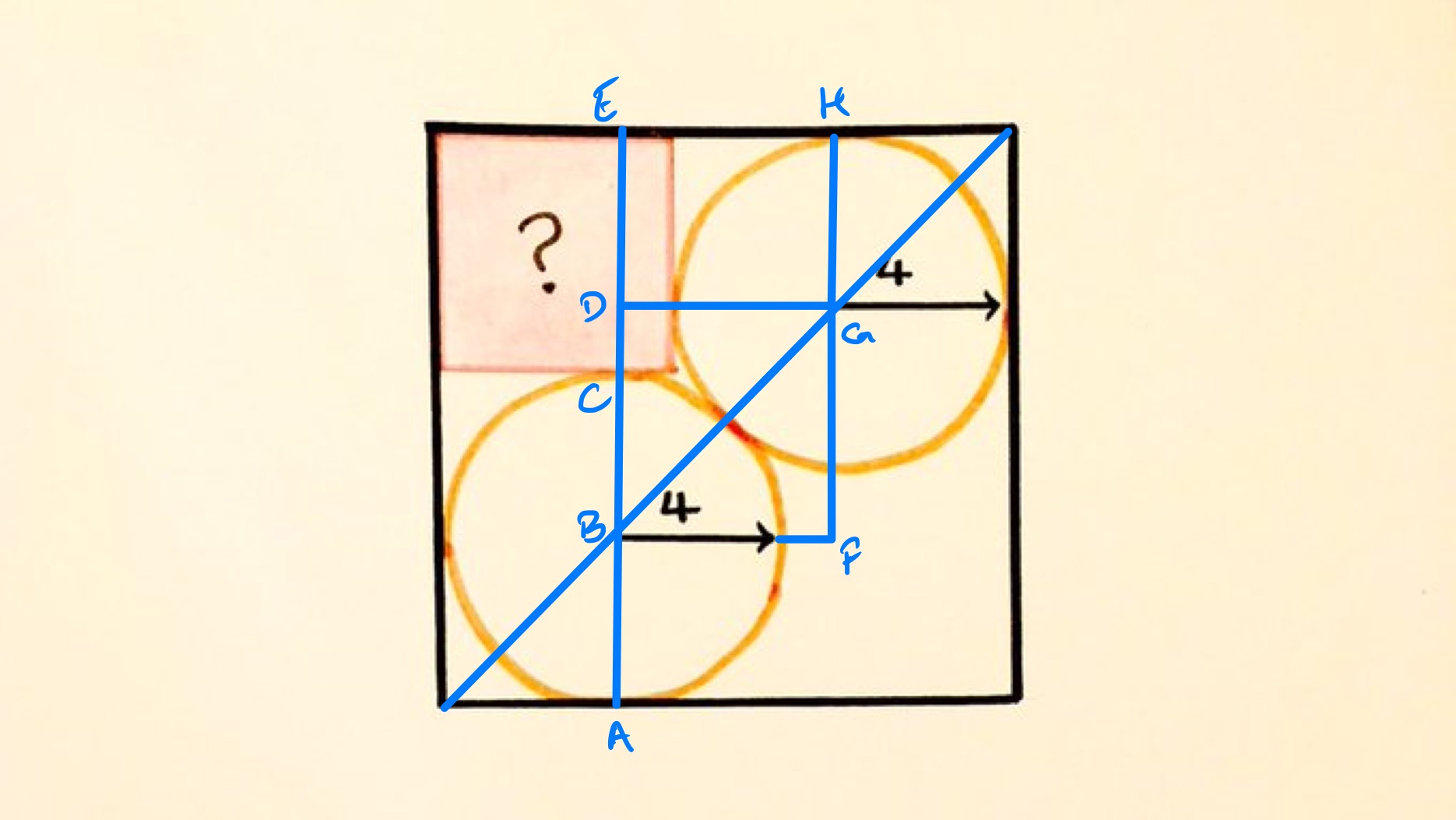
In the above diagram, the height of the square is the side length of the shaded square plus the length of and is also the combined lengths of , , and . Since both and are radii of the circles, this means that the height of the shaded square is the same as the length of . The shaded square is therefore congruent to . Since the area of a square is half the square of its diagonal, and the diagonal of is two radii of the circles, the area is .