Notes
triangles with a parallelogram solution
Triangles with a Parallelogram
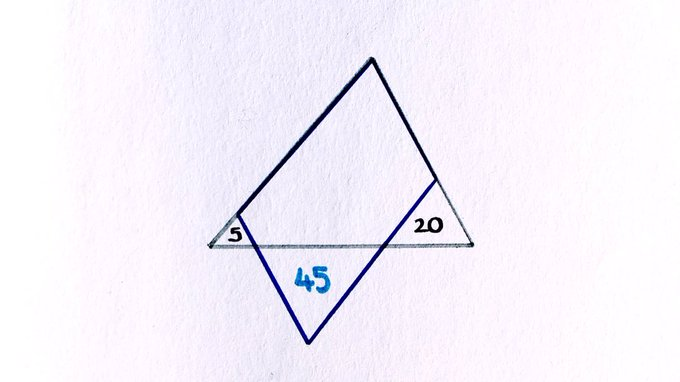
What’s the area of the parallelogram?
Solution by Similar Triangles and Area Scale Factor
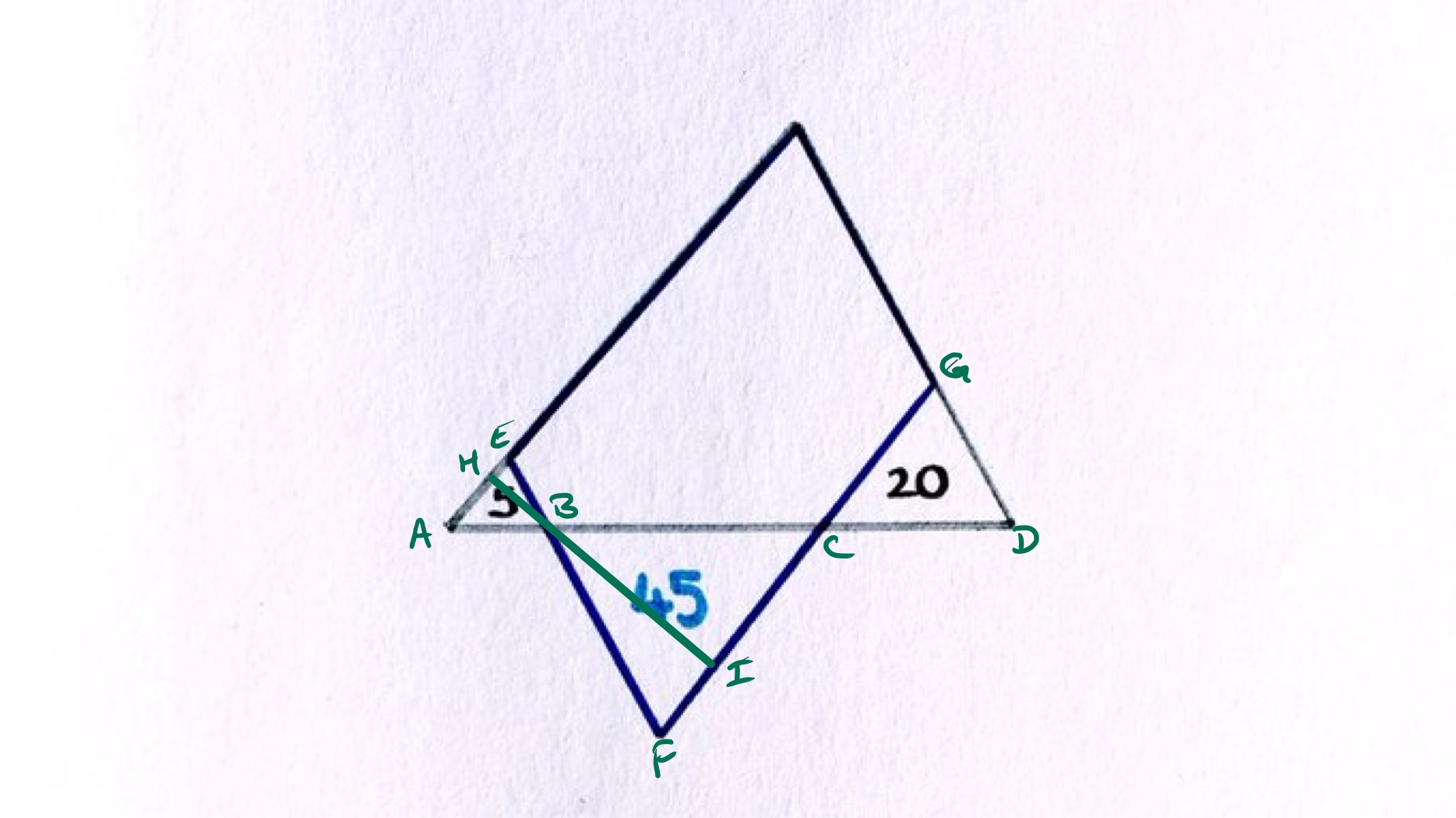
With the points labelled as above, the area of the parallelogram can be found by multiplying the lengths of and of .
The line segments and are parallel, and angles and are vertically opposite and so are equal. Therefore, triangles and are similar. The area scale factor is , so the length scale factor is . This means that the length of is times that of .
A similar argument applied to triangles and shows that is of .
Since the area of triangle is , multiplying the lengths of and gives . Therefore the area of the parallelogram is .