Notes
triangles in a semi-circle solution
Triangles in a Semi-Circle
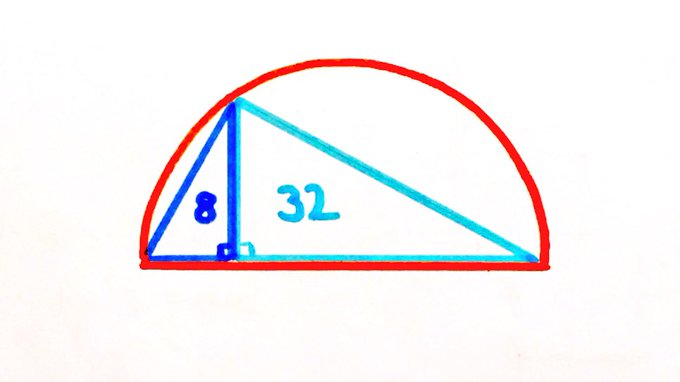
What’s the area of the semicircle?
Solution by Similarity
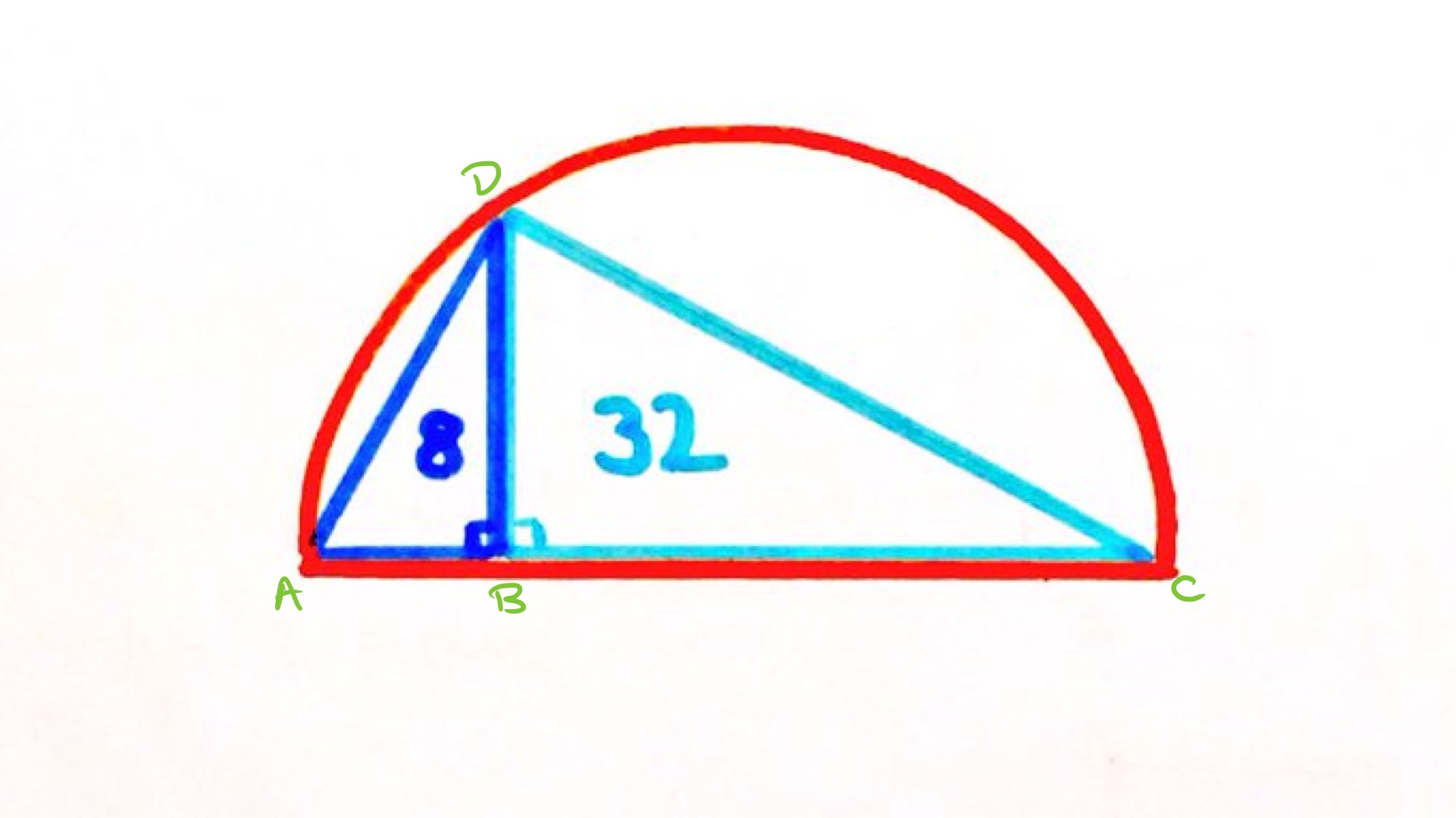
Triangles and are similar because they are both right-angled and the angles at add up to since it is the angle in a semi-circle. The area scale factor is , so the length scale factor is . This means that has twice the length of , and twice that of . Let be the length of , then has length and length .
The area of triangle is so . The area of the semi-circle is .