Notes
triangle over two rectangles solution
Solution to the Triangle Over Two Rectangles Puzzle
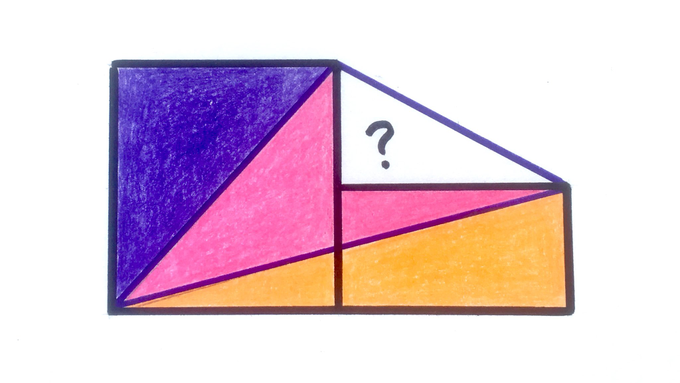
Each coloured region has area . What’s the area of the upper triangle?
Solution by Area of a triangle
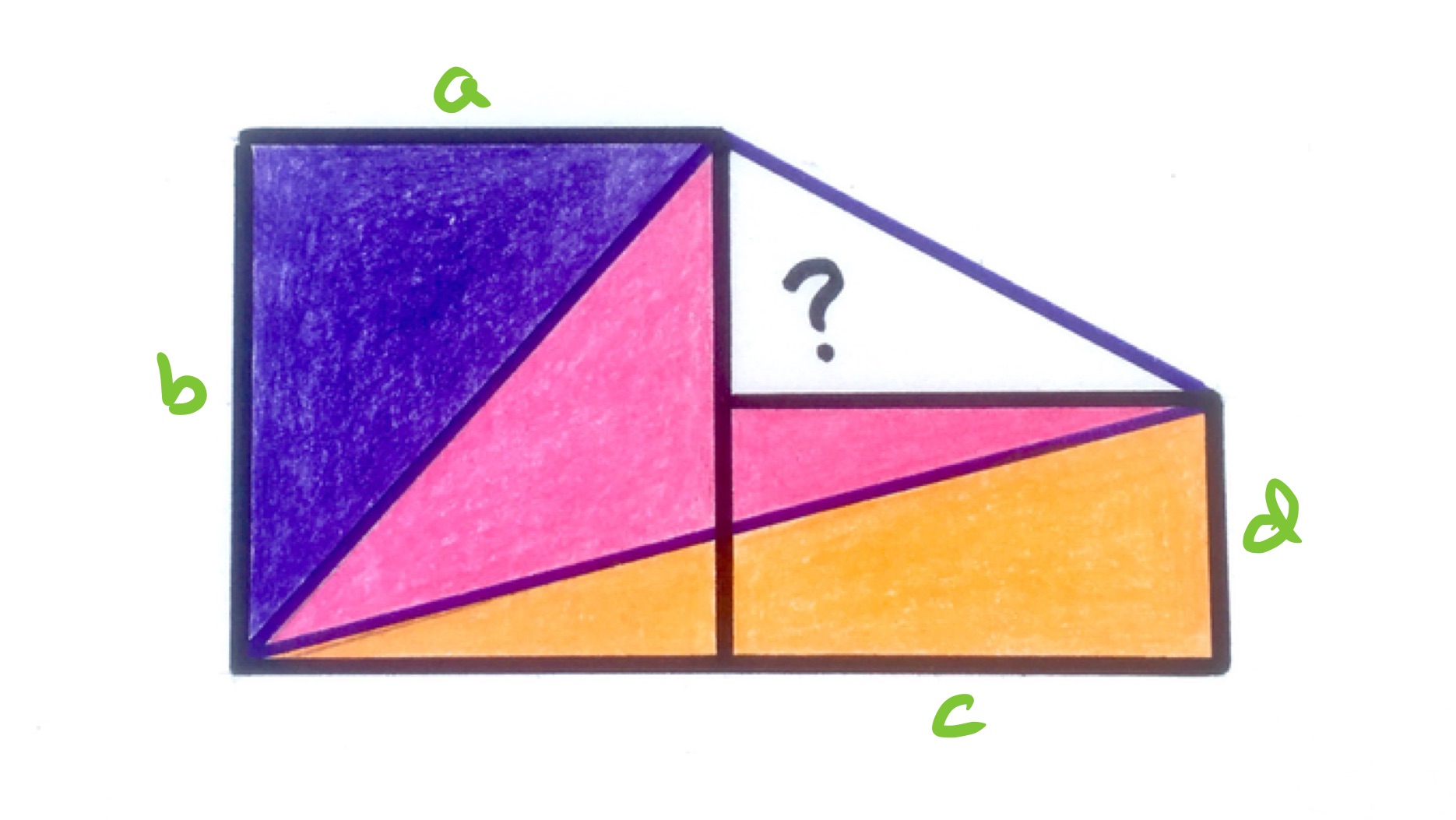
With the lengths as in the above diagram, the areas are as follows:
- Orange:
- Purple:
- Pink:
- White:
Simplifying the area of the pink region leads to the expression:
Since the pink and purple regions have the same area, the last two terms in this expression must cancel out and so . Putting this into the expression for the orange region gives that as and so as this is the same as the area of the purple region it must be that . The expression for the area of the white region therefore simplifies to which is half the area of the purple region and so the upper triangle has area .
Solution by Dissection
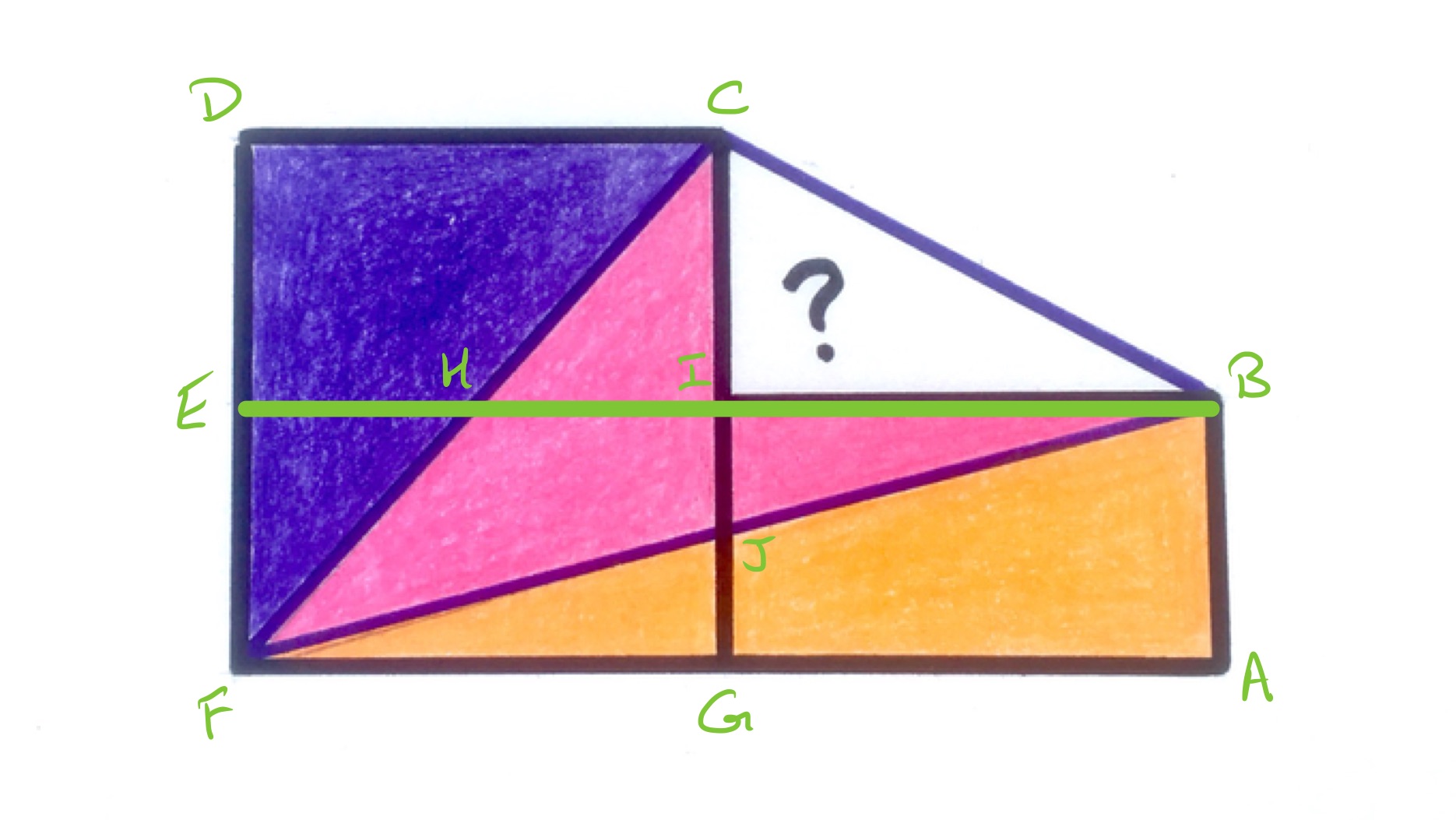
In the above diagram, triangles and are congruent and so the same area. As each coloured region has the same area, this means that the triangles and have the same area. They are also similar since they are right-angled triangles and angles and are the same as they are vertically opposite angles. They are therefore congruent. This means that and have the same length and so is the midpoint of .
The height of triangle is therefore twice that of so since they have the same area, the base of must be twice the base of . That is to say, the length of is half that of . So then the length of is half that of .
Putting that together, the lengths of and are the same, while that of is half that of , so the area of triangle is half that of triangle , and so has area .