Notes
triangle inside circle and triangle solution
Solution to the Triangle Inside Circle and Triangle Puzzle
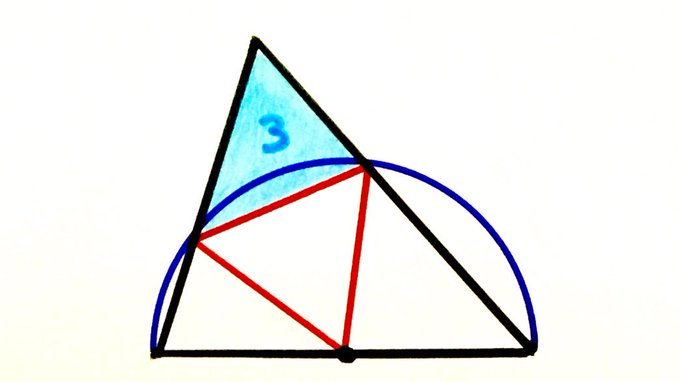
One corner of the equilateral triangle is at the centre of the semicircle. What’s the total area of the large black triangle?
Solution by Angles in a Cyclic Quadrilateral, Angles at a Point on a Straight Line, and Similar Triangles
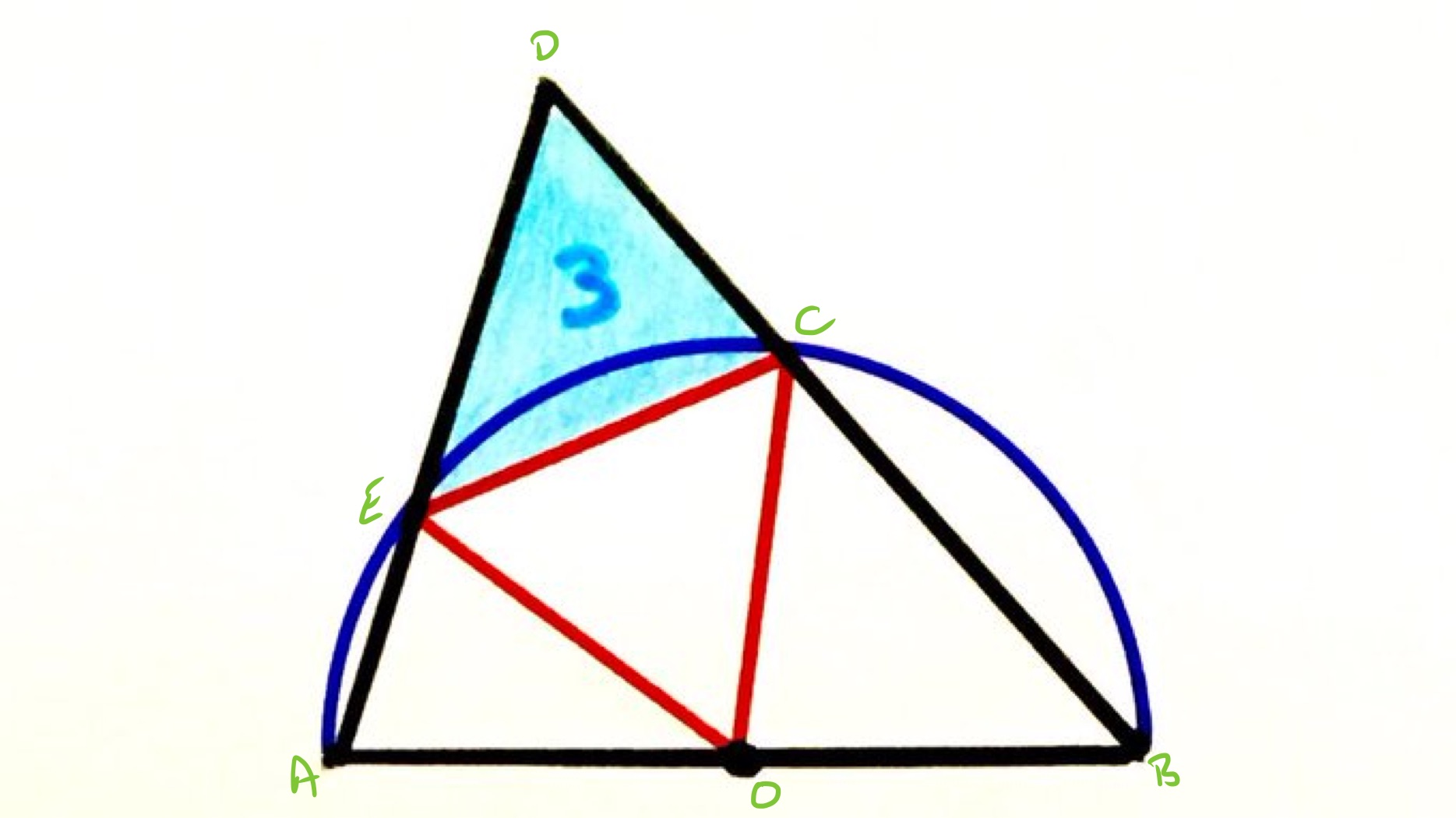
With the points labelled as above, angles and add up to as they are the opposite angles in a cyclic quadrilateral, so angle is the same as angle since angles at a point on a straight line also add up to . Similarly, angles and are equal. So triangles and are similar, with corresponding to and to . The scale factor comes from comparing with : since has length equal to a radius of the semi-circle and is a diameter, the scale factor is . Therefore triangle has are four times that of , so has area .