Notes
triangle inside a square solution
Solution to the Triangle Inside a Square Puzzle
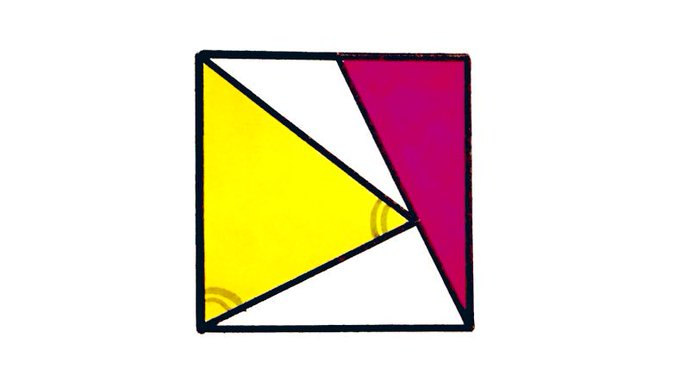
The right-angled triangle covers of the square. What fraction does the isosceles triangle cover?
Solution by Angle in a Semi-Circle and Similar Triangles
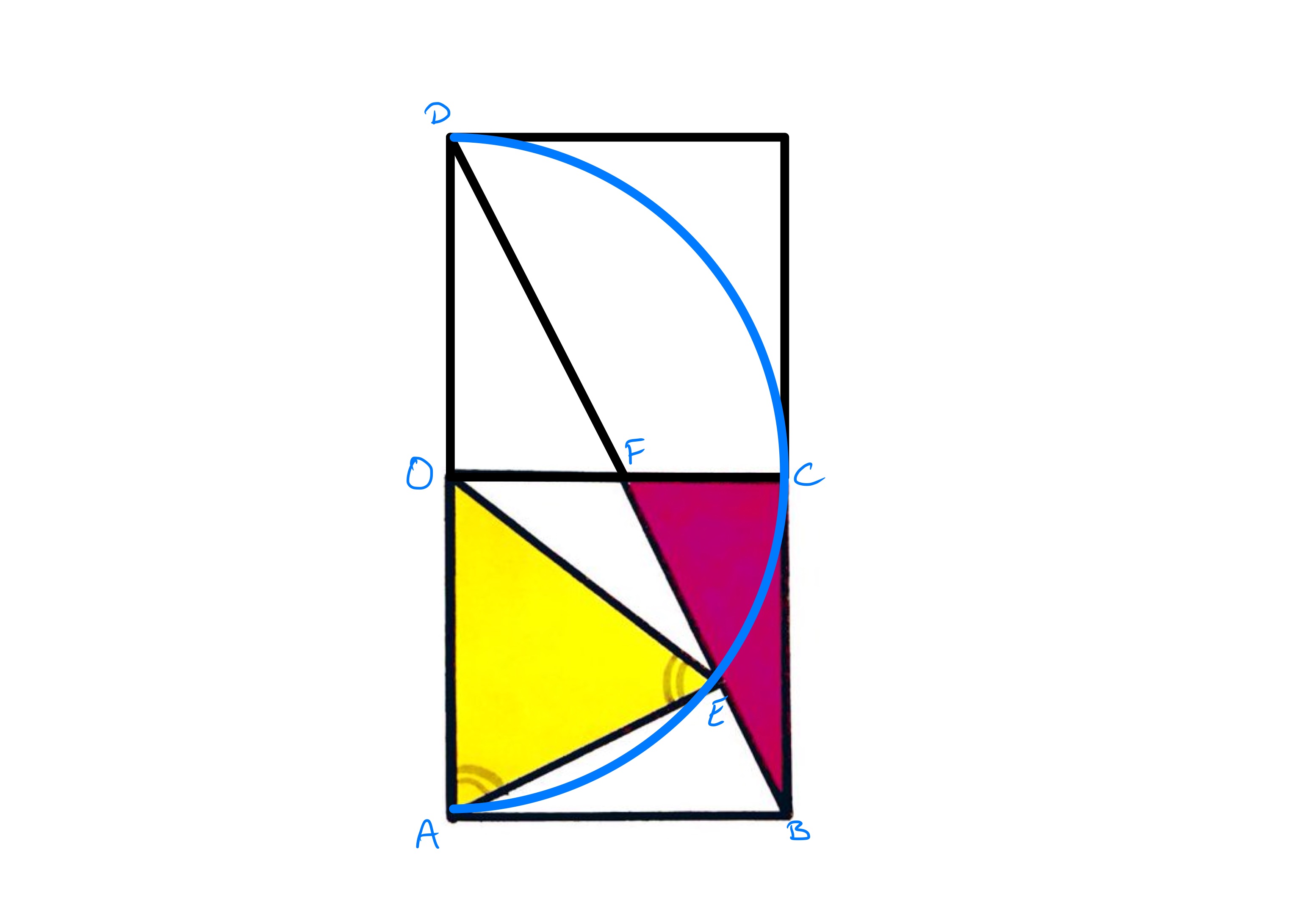
In the above diagram, a second square has been placed on top of the original one. As , , and are all the same length, the circle centred at that passes through also passes through and . Since triangle is isosceles, it also passes through .
Triangles and have the same area since their “bases” and have the same length and they have the same apex, , above the line . So triangle has half the area of triangle .
Triangle is right-angled since the angle in a semi-circle is and is similar to triangle . So also is triangle . Since the length of is twice that of , the length of is twice that of , and that of is twice that of . So has length four times that of , meaning that triangle is four fifths of triangle . Hence triangle is two fifths of triangle . Since triangle has the same area as the original square, the yellow triangle has area ths of that square.