Notes
triangle in two tilted squares solution
Solution to the Triangle in Two Tilted Squares Puzzle
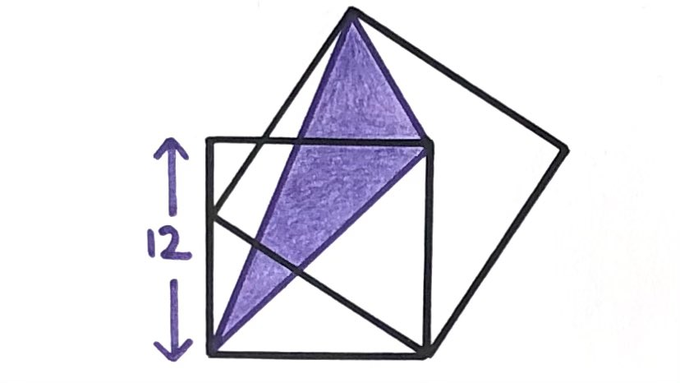
Two squares. What’s the shaded area?
Solution by Transformations
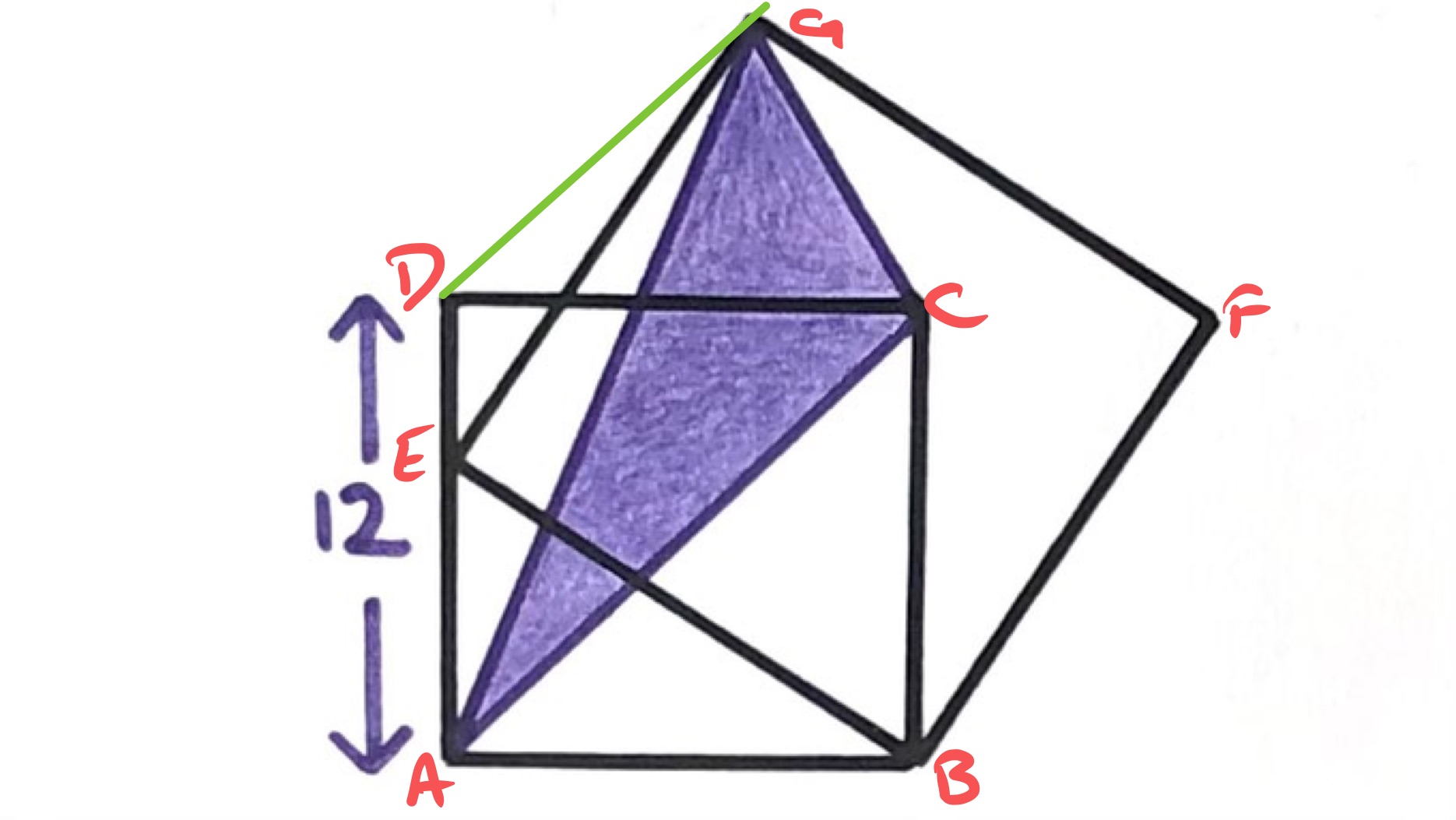
The vertex is free to move on the line . The vertex is the image of after a combined transformation of a scaling by scale factor and a rotation clockwise by . It therefore also moves on a line. When is at , is at . When is at , the square is tilted at . So moves along a line that is at to the horizontal passing through . This line is parallel to , which we can view as the “base” of the triangle , and so the area of the triangle is independent of where the point is on this line. In particular, if it is at then the area of the triangle is evidently half of the area of the square, and thus is .
Solution by Invariance Principle
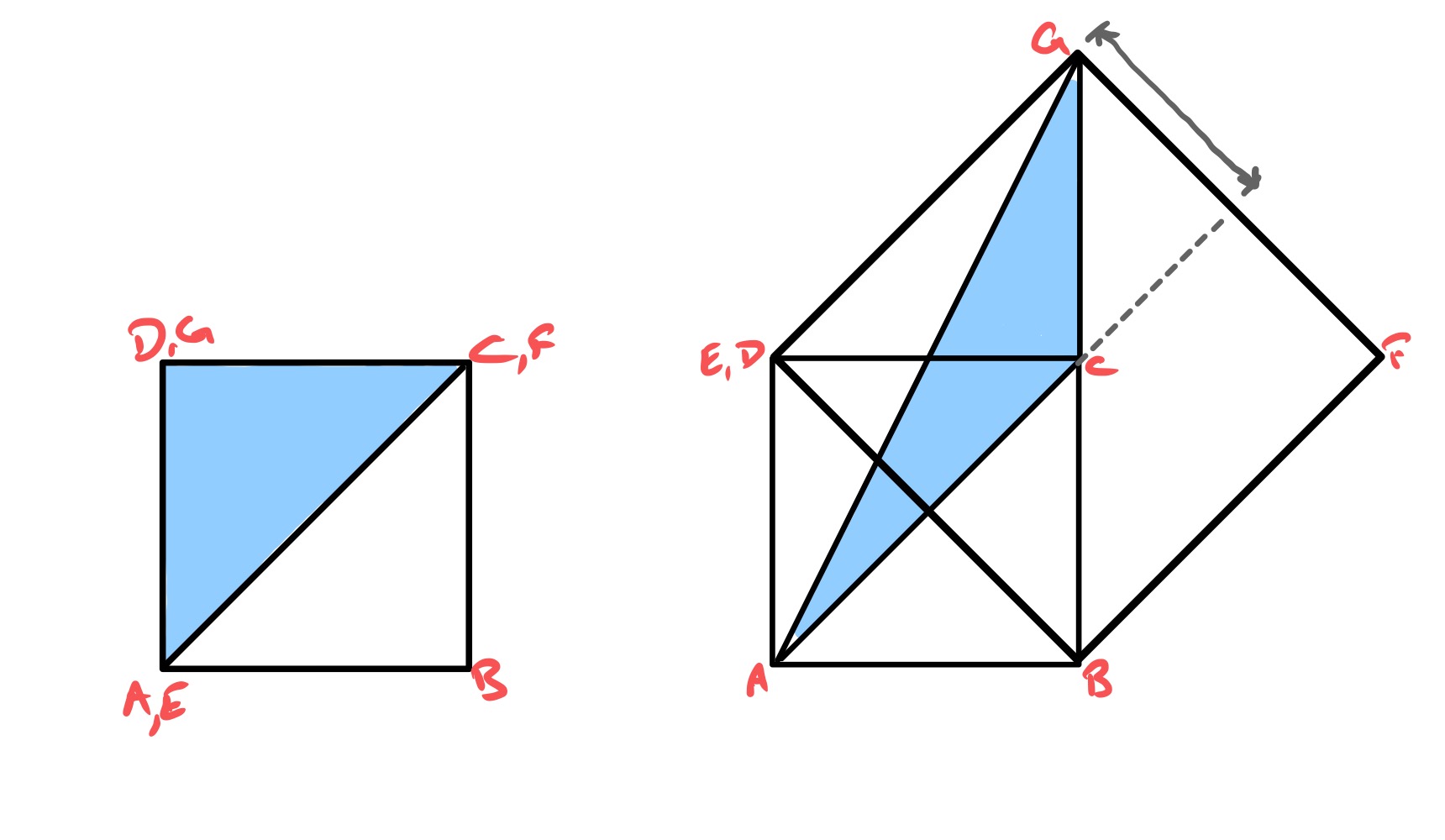
There are two special cases of this problem: when the vertex is at and when it is at . If it is at , is at and the area is half of that of the square, whence . If it is at then the height of the triangle above is half of and so again the area of the triangle is half of that of the smaller square.