Notes
triangle in four rectangles solution
Triangle in Four Rectangles
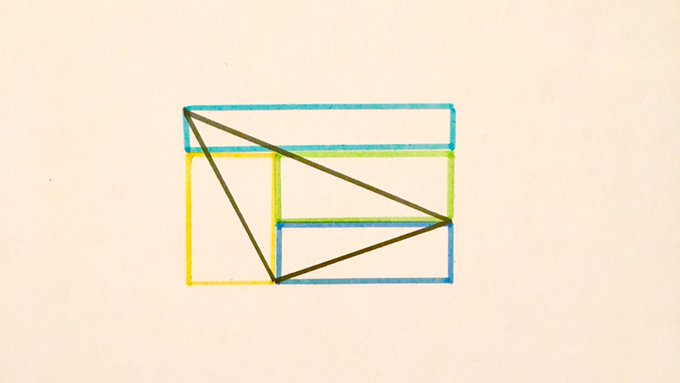
The four rectangles each have area . What’s the area of the triangle?
Solution by Area of a Rectangle and Area of a Triangle
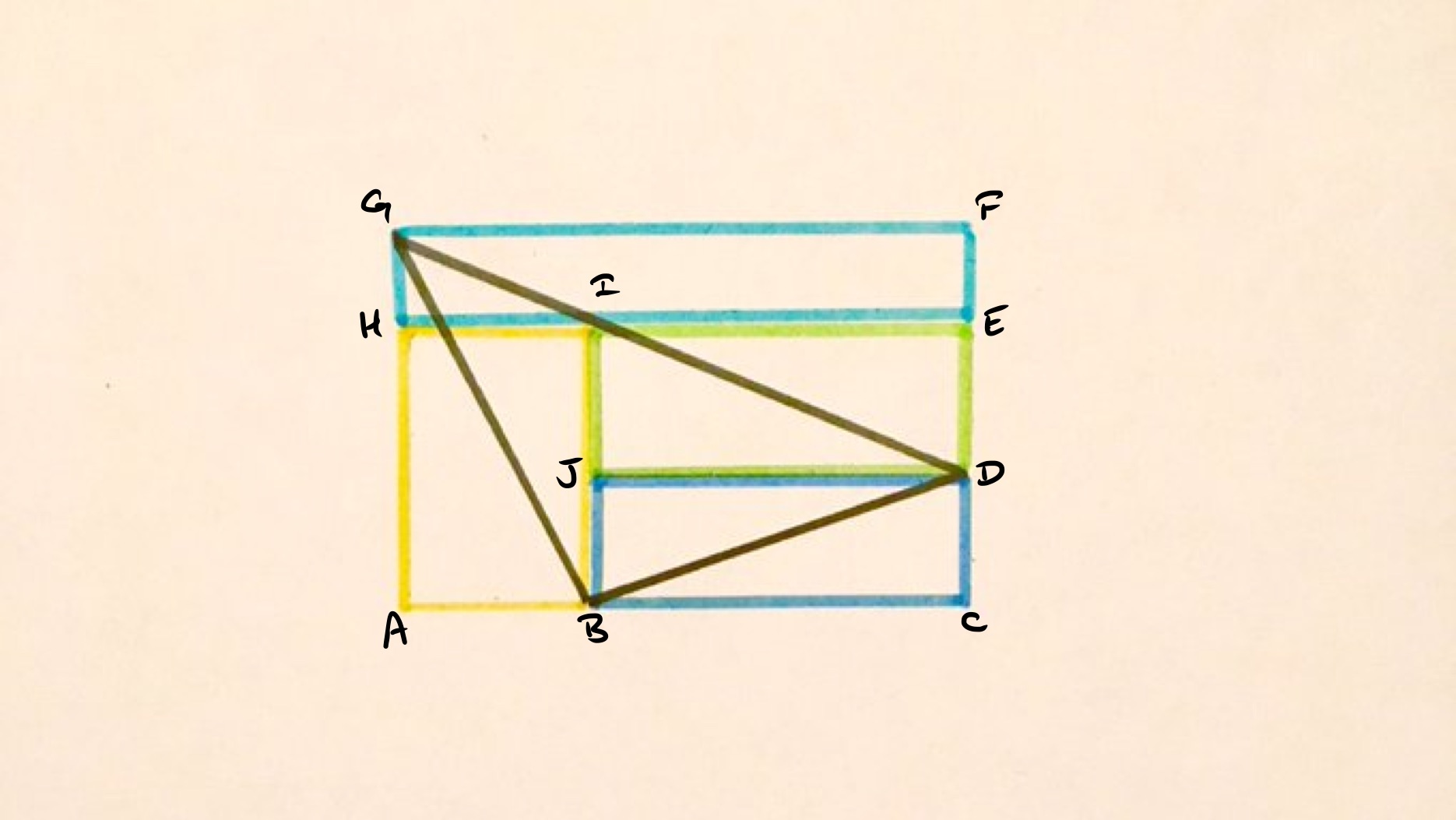
With the points labelled as above, rectangles and have the same width, so since they have the same area then they must have the same height. Then rectangle has twice the height of these rectangles, so its width is half. That is, the length of is half that of . Finally, the width of is three times that of , so the height of is one third of that of .
Let be the length of , and the length of . Then has length and has length . The length of is one third of that of , so is . As the area of each rectangle is then so .
Triangle has base and height so has area . Triangle has base and height so has area . Triangle has base and height so has area . The total area of these triangles is . The total area of the rectangle is . This leaves for the central triangle.