Notes
triangle in a rectangle solution
Solution to the Triangle in a Rectangle Puzzle
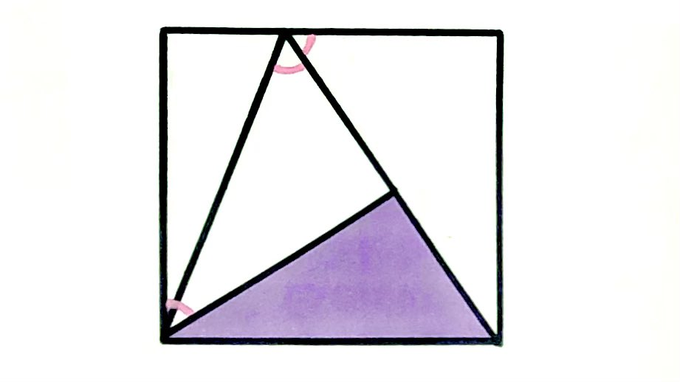
The three marked angles are equal. What fraction of the rectangle is shaded?
Solution by Angles in parallel lines, Angles in a Triangle
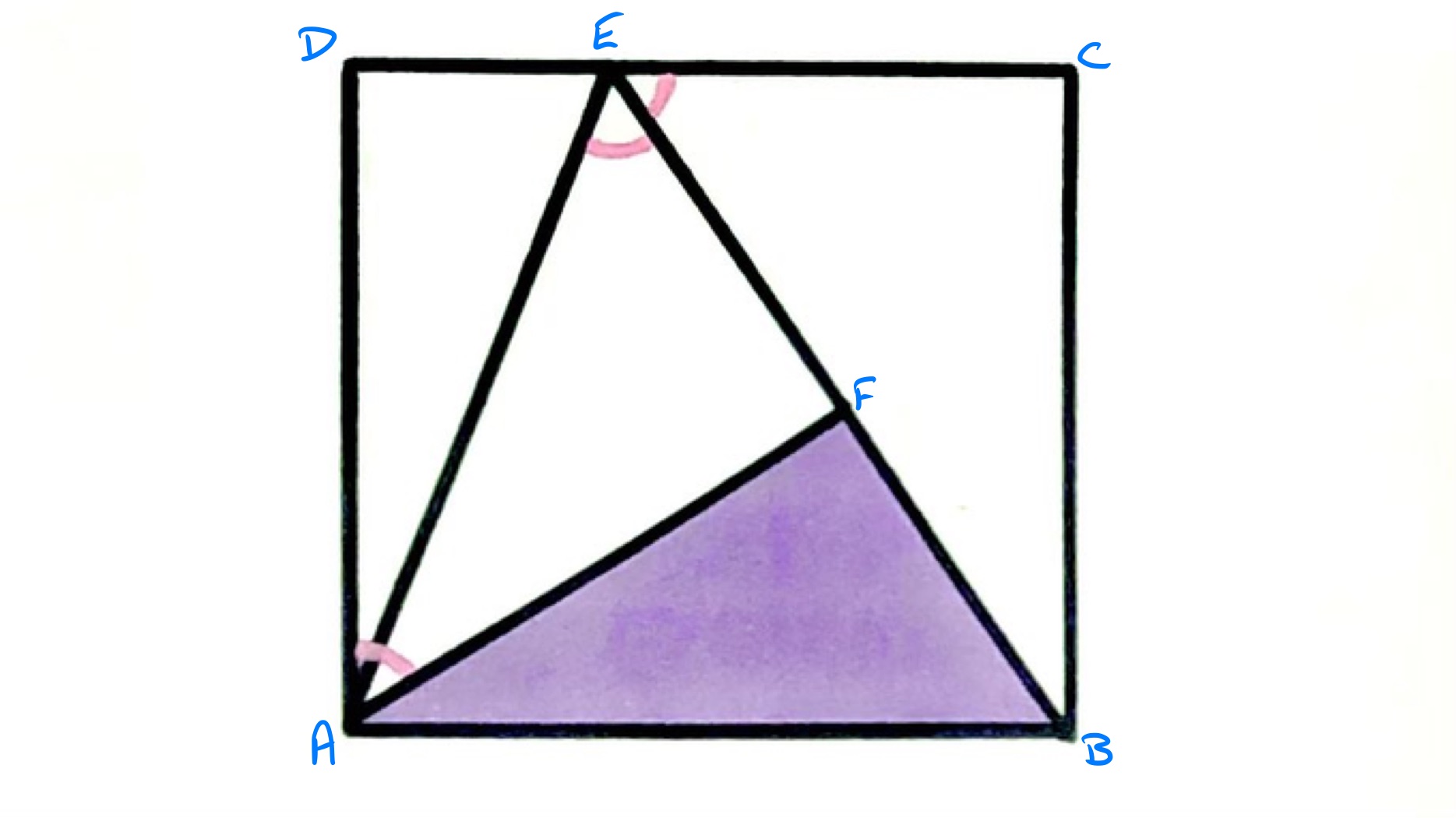
Using alternate angles, angle is equal to angle and so triangle is isosceles. Angles and add up to , so since angles and are equal, angles and add up to meaning that angle is since angles in a triangle add up to .
Since triangle is an isosceles triangle and angle is a right-angle, is the midpoint of . This means that the height of above is one half of the height of . This establishes the shaded area as one quarter of the area of the total rectangle.
Solution by Invariance principle
One way to see the variation in this puzzle is to start with the angle . The rest of the diagram can be constructed starting with this angle.
Fix a horizontal line and a point on it. The point will also lie on this line and to the right of , so it can be used to label the angle unambiguously even before its location is fully determined. Choose a point below the line and to the left of so that angle is obtuse. Let be on the line so that angle is a right-angle. The point lies on the angle bisector of angle so that is parallel to . Then is so that angle is a right-angle. Finally, is the point on such that angle is half of angle .
Two special cases that make the answer simpler to see are when angle and when it is .
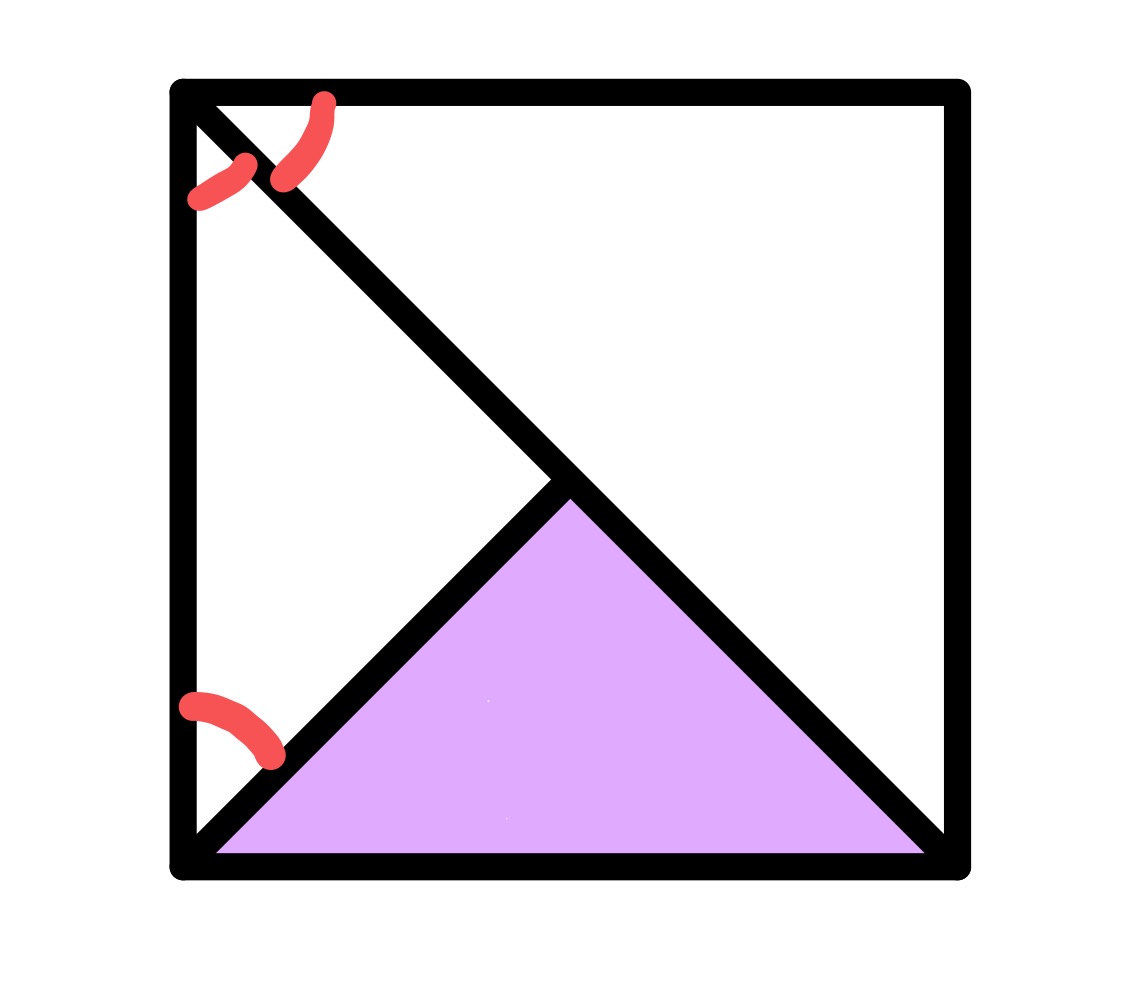
When angle , the highlighted angle is and the rectangle is a square. The highlighted area is one quarter of that square.
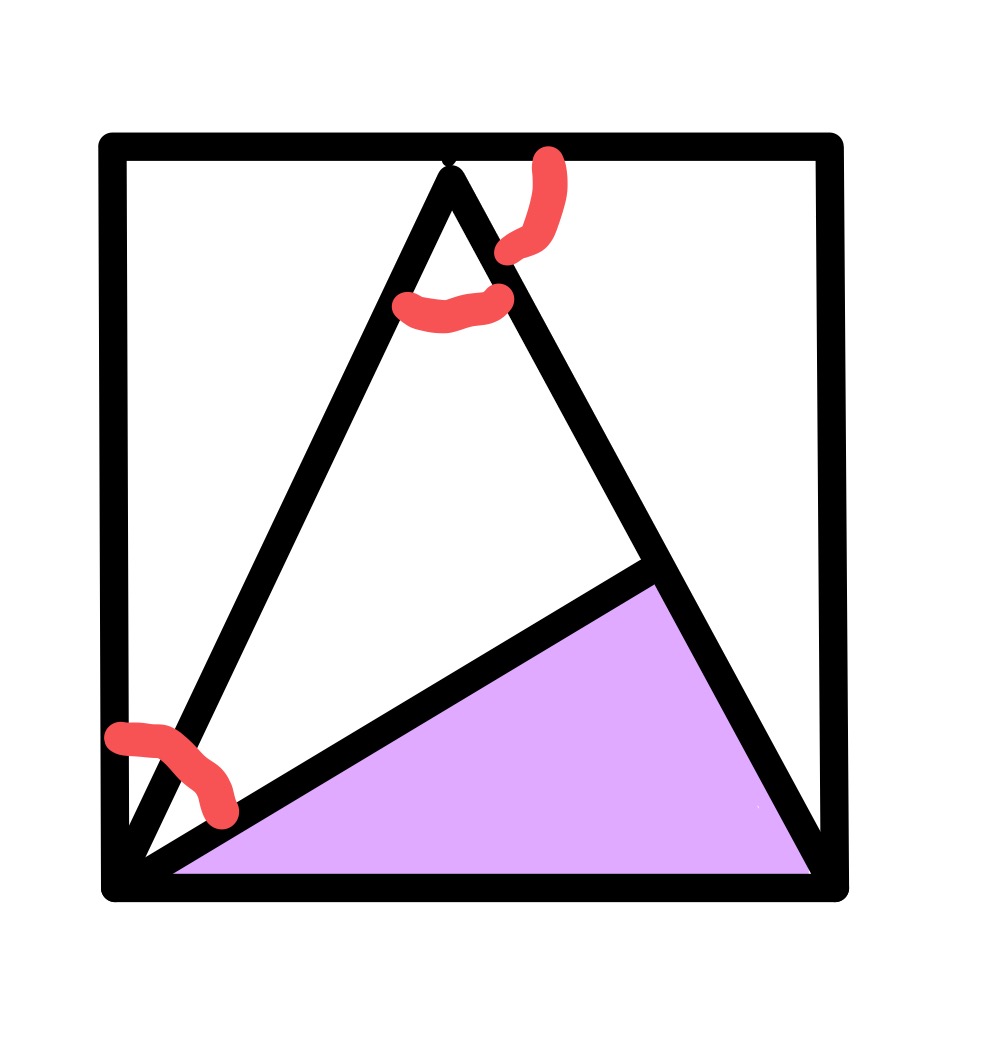
When angle , the highlighted angle is and the inner triangle is equilateral. The four smaller triangles (of which the shaded triangle is one) are all congruent triangles and so the shaded area is one quarter of the total area.