Notes
triangle in a circle in a quarter circle in a square solution
Solution to the Triangle in a Circle in a Quarter Circle in a Square Puzzle
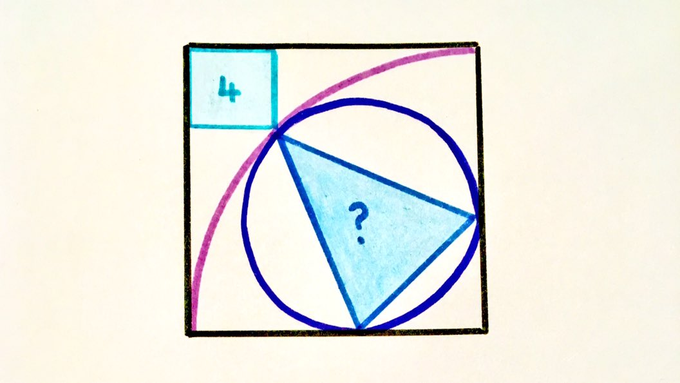
The area of the small square is . What’s the area of the triangle?
Solution by Angle Between a Radius and Tangent, Lengths in an Isosceles Right-Angled Triangle
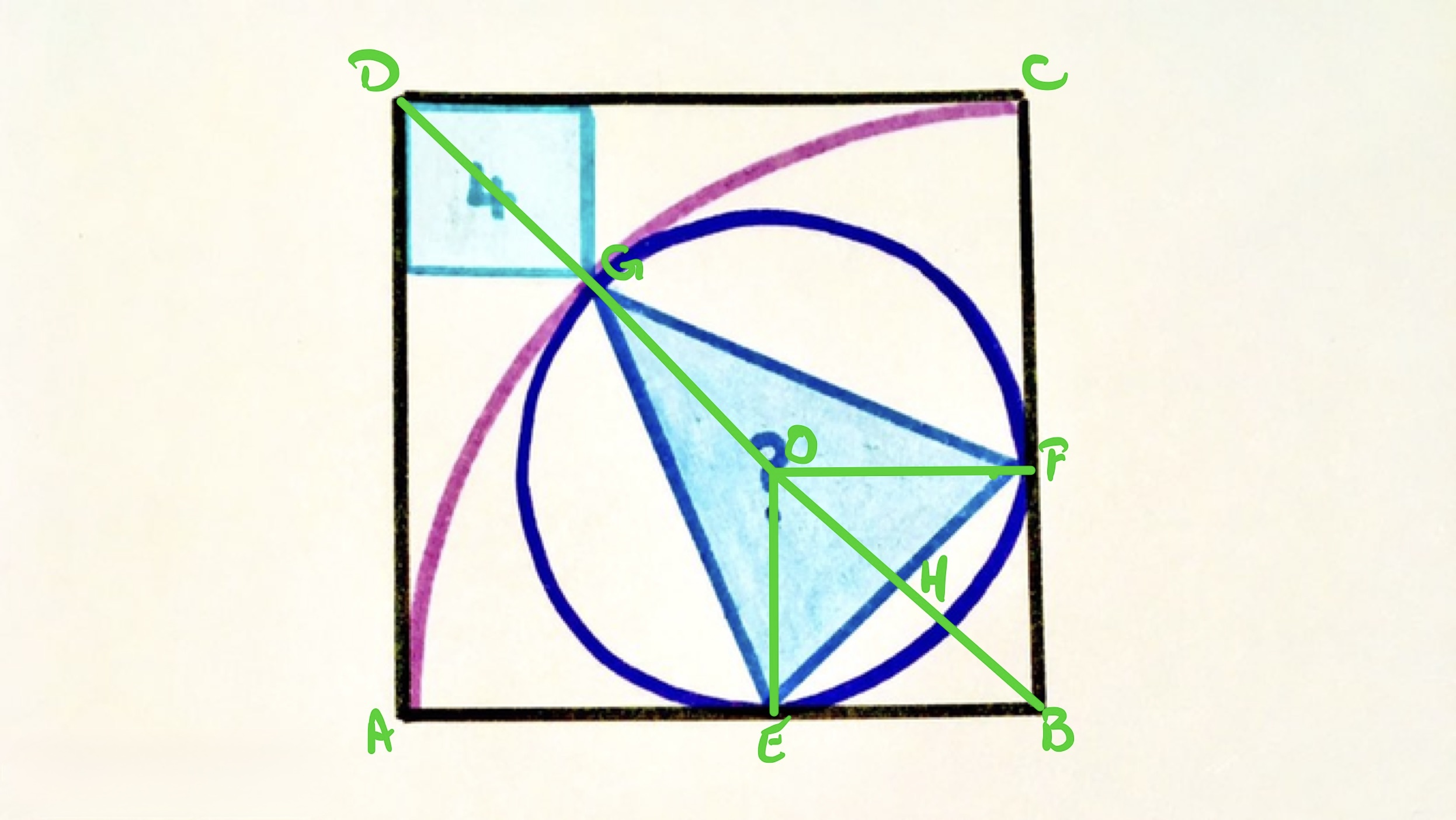
With the points labelled as above, let be the radius of the inner circle and the side length of the outer square. Then has length , and is the diagonal of the square so has length . Therefore, the length of is . This is also the diagonal of the square of area , so:
and hence .
Since the angle between a radius and tangent is , angles and are , so is a rectangle, but since and are both radii of the circle they are the same length and so is a square. Hence has length , so has length and thus:
and hence , and then has length .
Since is also a diagonal of square (and so also has length ), it bisects and so has length . Therefore has length , so triangle has area: