Notes
triangle centres and square corners solution
Triangle Centres and Square Corners
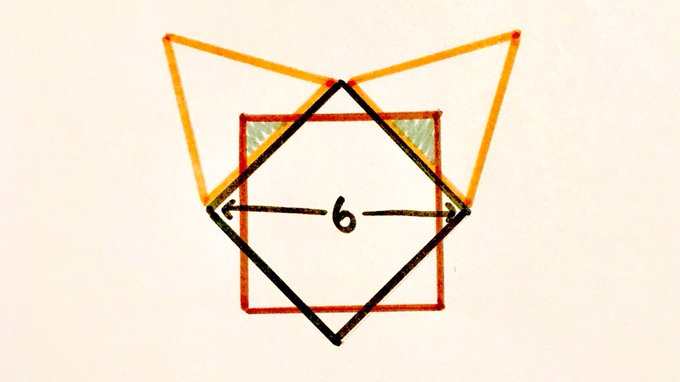
The corners of the red square are at the centres of the equilateral triangles. What’s the total shaded area?
Solution by Properties of Squares and Lengths in Equilateral Triangles
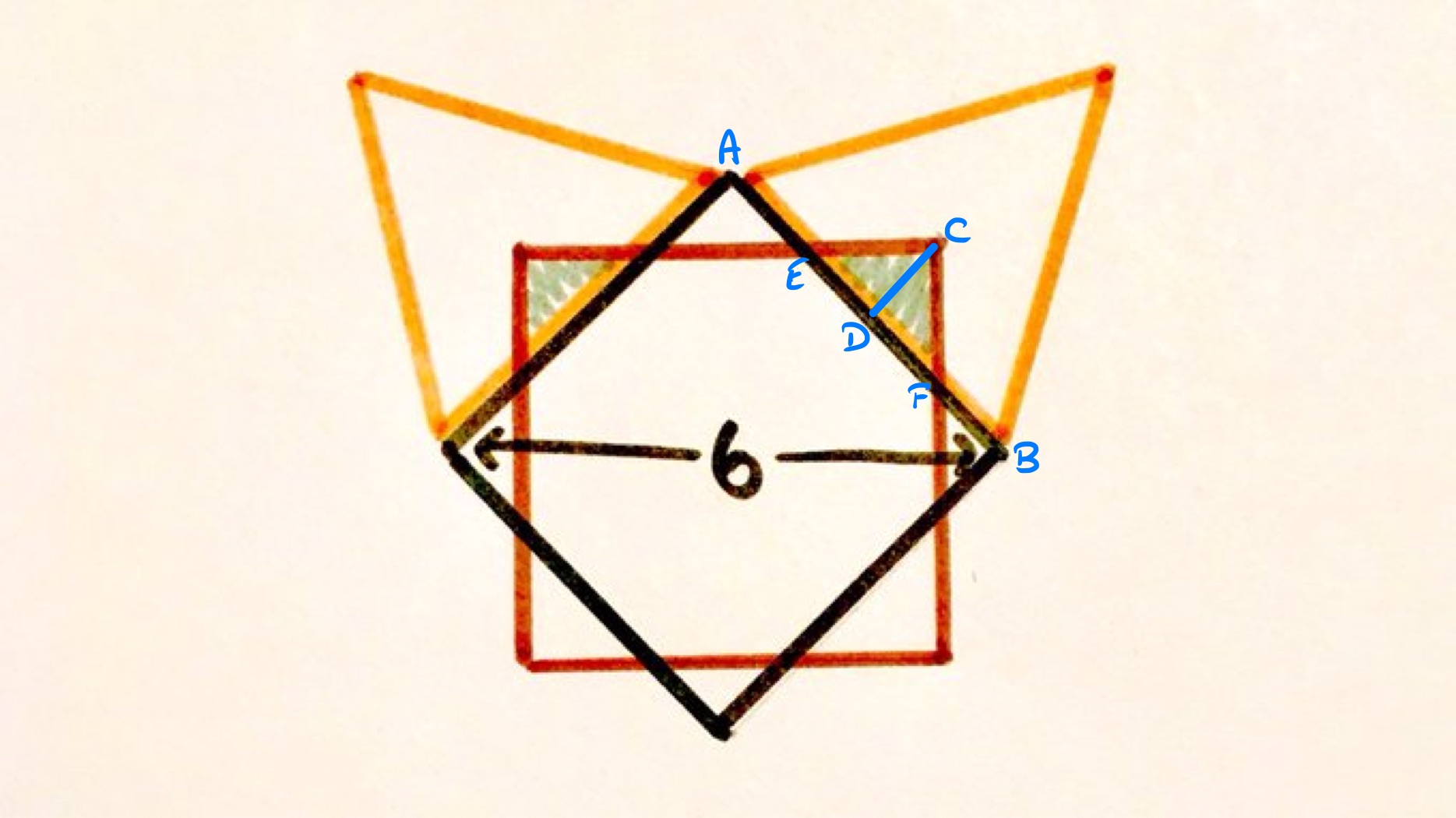
As the diagonal of the square is , the side length is . This is also the side length of the equilateral triangles. Using the relationship between the lengths in an equilateral triangle, the length of is . Triangle is an isosceles right-angled triangle, so has the same length as . The area of triangle is then . The shaded region comprises four of these triangles, so it has area .