Notes
triangle and circle inside square solution
Solution to the Triangle and Circle Inside Square Puzzle
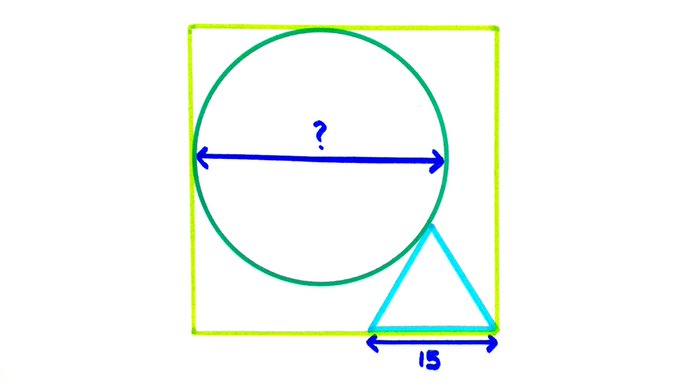
The equilateral triangle in the corner of this square is tangent to the circle where they touch. What’s the diameter.
Solution by Angles in an Equilateral Triangle, Angle Between a Radius and Tangent, Angles in a Triangle, and Isosceles Triangles
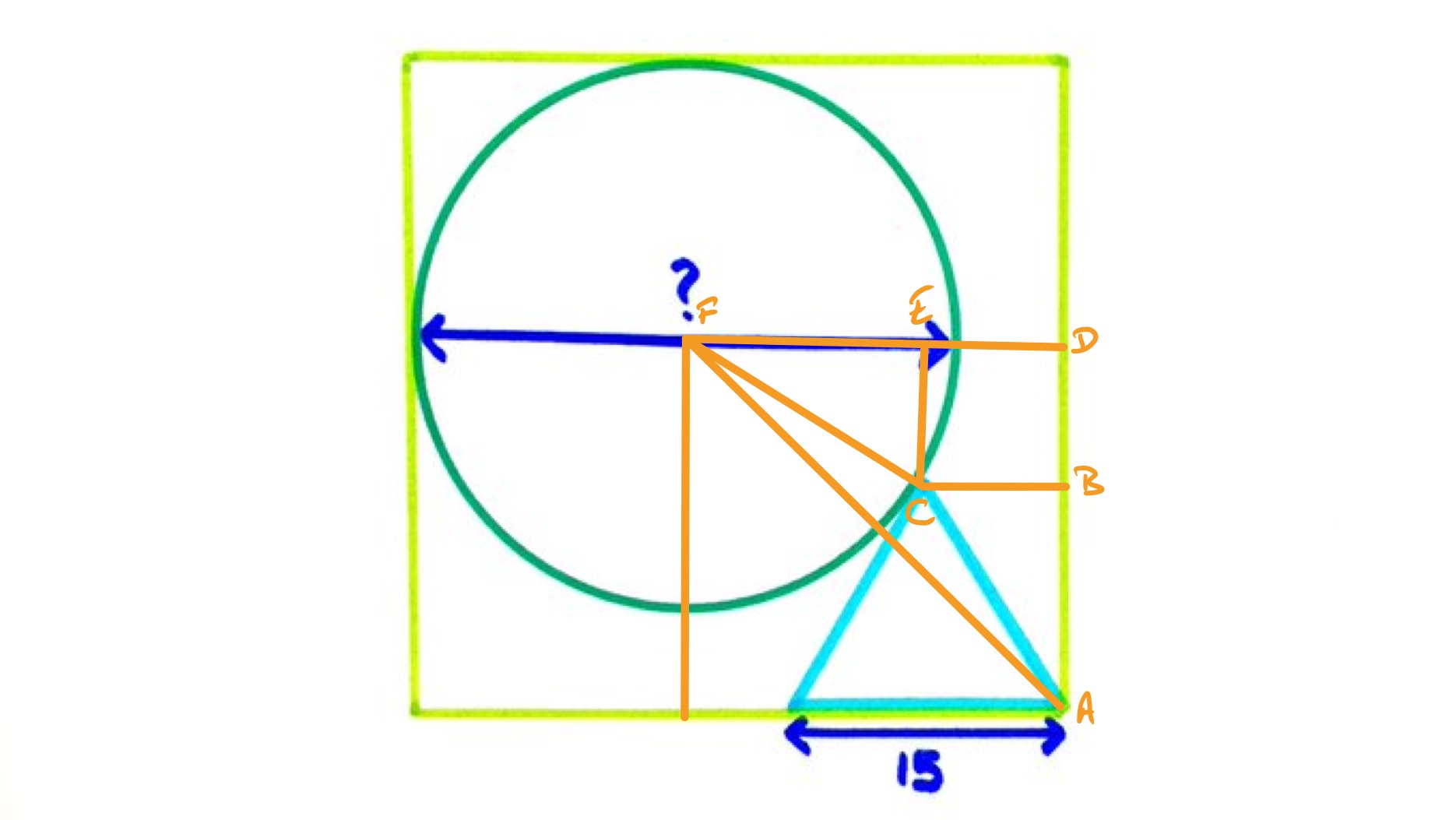
With the points labelled as above, first note that point lies on a diagonal of the square since the circle touches two sides. Therefore, angle is . Since the interior angle in an equilateral triangle is , angle is and so angle is .
As the angle between a radius and tangent is , angle is . This leaves for angle as the angles in a triangle add up to . So triangle is isosceles and hence and have the same length. The diameter of the circle is therefore .