Notes
toppled square solution
Toppled Square
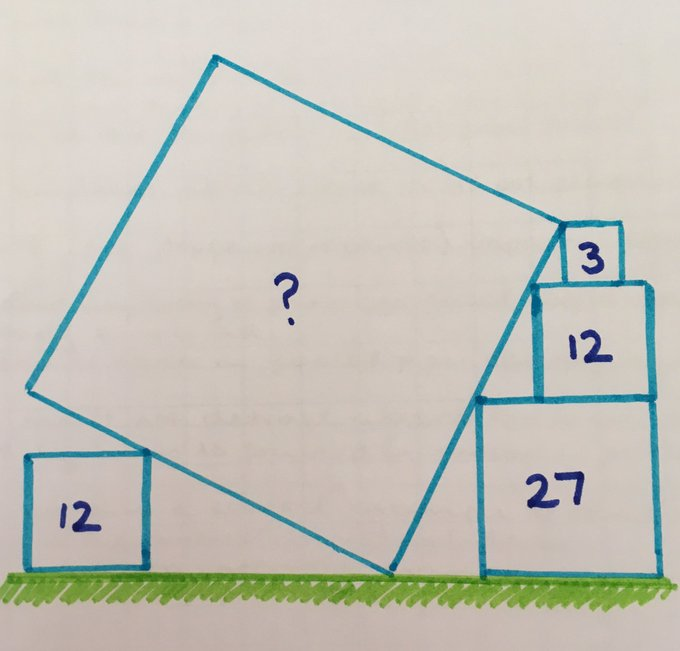
What’s the area of the toppled square?
Solution by Pythagoras' Theorem
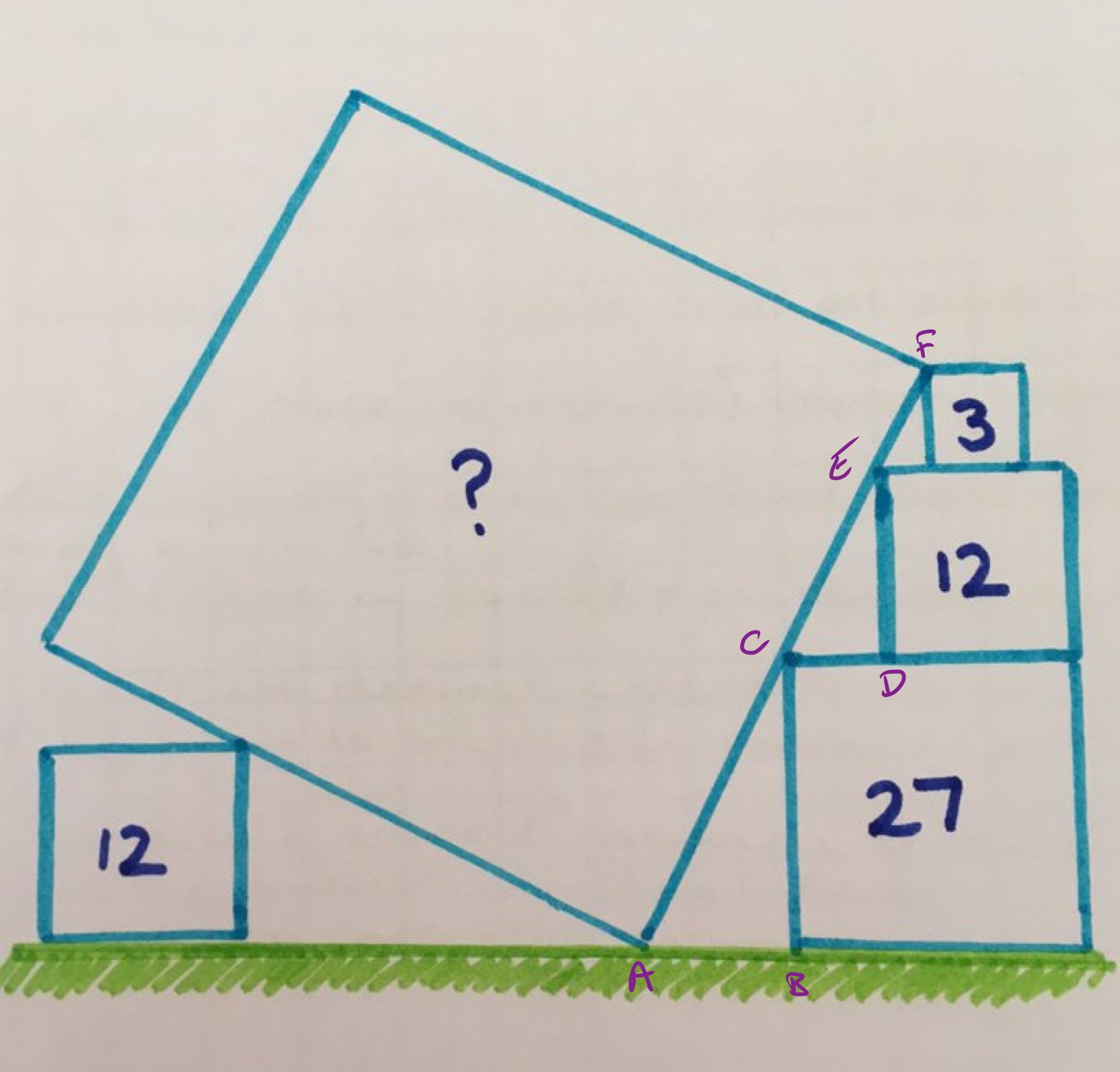
The heights of the three squares on the right-hand side are , , and . Therefore the total height of above the base is .
The length of is and of is . Let be the length of then applying Pythagoras' theorem to triangle shows that so . Since the height of above the base is times the length of , the length of is . Therefore the area of the large square is .