Notes
tilted rectangles solution
Solution to the Tilted Rectangles Puzzle
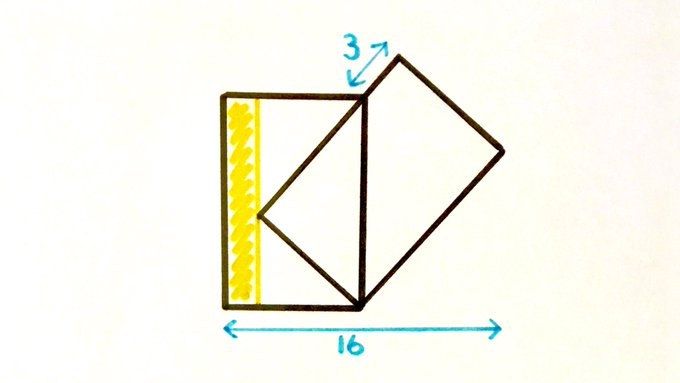
The two rectangles are congruent. What’s the shaded area?
Solution by Area of a Parallelogram
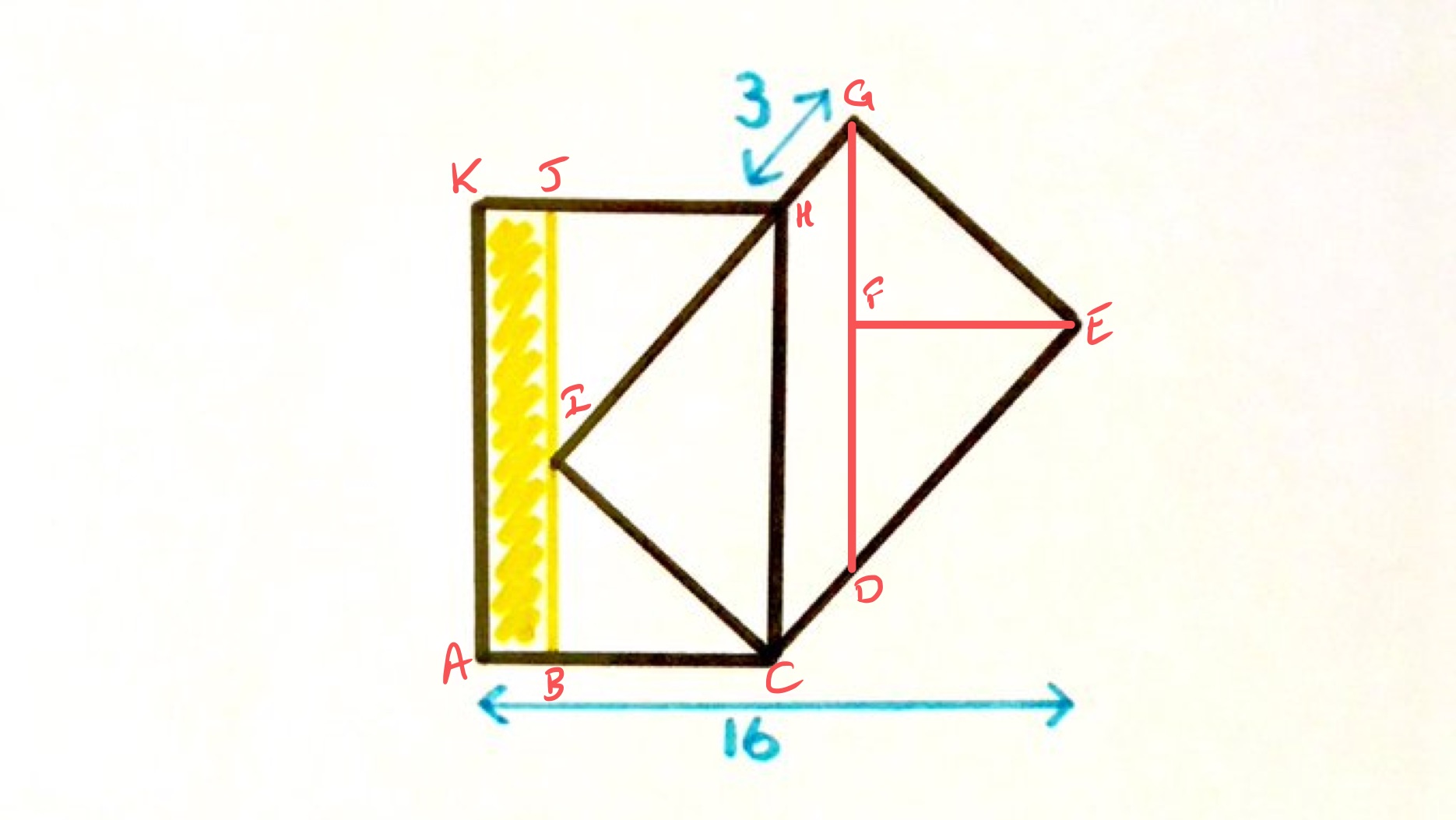
With the points labelled as above, triangles and are congruent as are triangles and . This means that the yellow rectangle, , and the parallelogram have the same area.
Thinking of as the base of this parallelogram, as this is the same as the height of the rectangle, the horizontal width of the parallelogram must be the same as that of the yellow rectangle. Since has the same length as , this means that the horizontal distance of from is the same as the length of . So has length .
Now thinking of as the base of the parallelogram, its “height” above this base is the length of , which is . Therefore the area of the parallelogram is .
Since the parallelogram and yellow rectangles have the same area, the shaded region has area .