Notes
tilted rectangle in a square solution
Tilted Rectangle in a Square
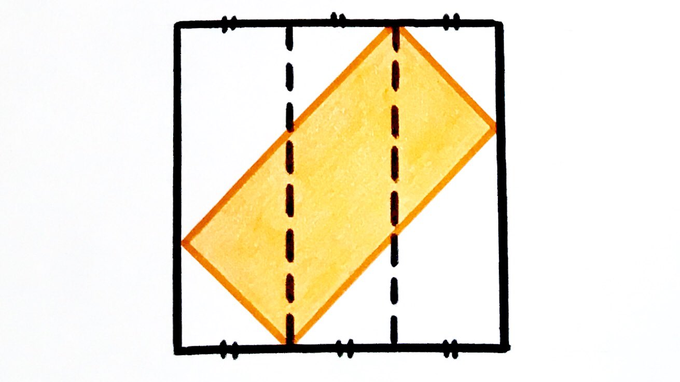
What fraction of the square does this rectangle cover?
Solution by Symmetry
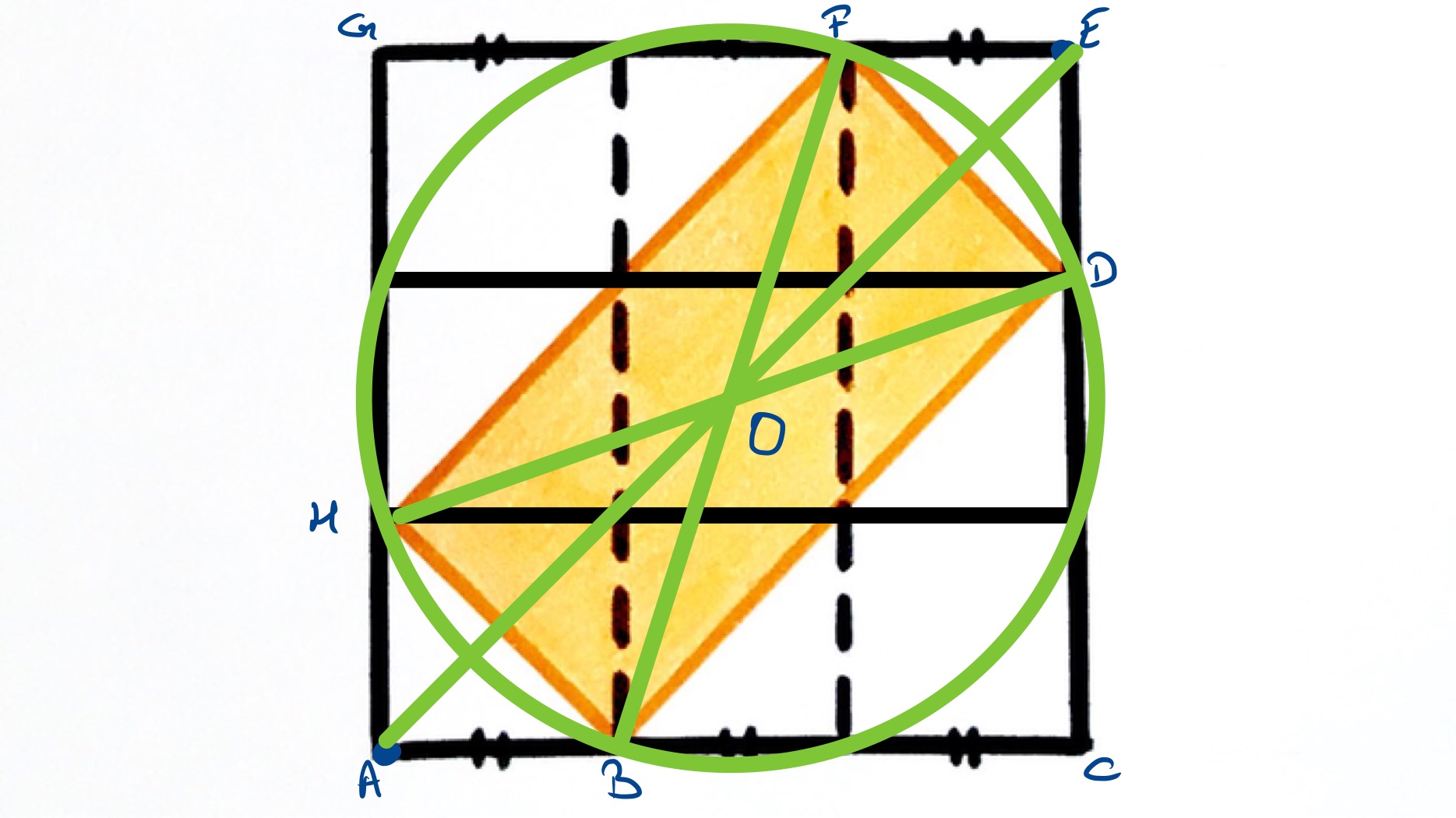
With the points labelled as in the above diagram, point is the centre of the rectangle.
As is the same way along as is along , the line is centrally placed in the square and so its midpoint, which is , is the same as the centre of the square. Therefore the circle centred on sits symmetrically in the outer square and so the points where it intersects with the square are proportionally the same along each side. This means that and are also one third of the way along their respective sides.
An alternative way to see this is to consider the triangles and . The sides and are the same length, and the angles at and are the same. This shows that and are the same length.
From the grid, the shaded area covers four of the smaller squares and so the fraction of the square covered by the rectangle is .