Notes
three triangles in a hexagon solution
Solution to the Three Triangles in a Hexagon Puzzle
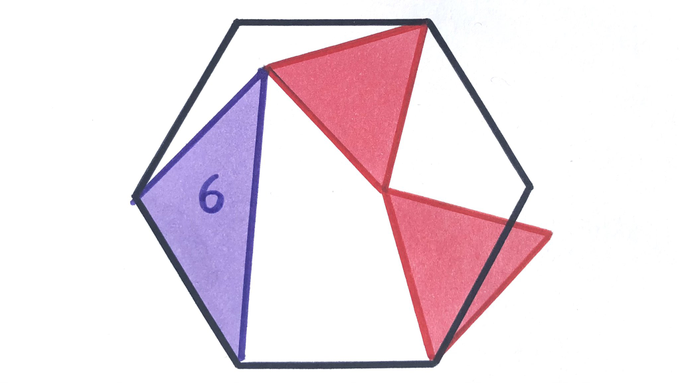
The two equilateral triangles are the same size. What’s the area of the regular hexagon?
Solution by Transformations
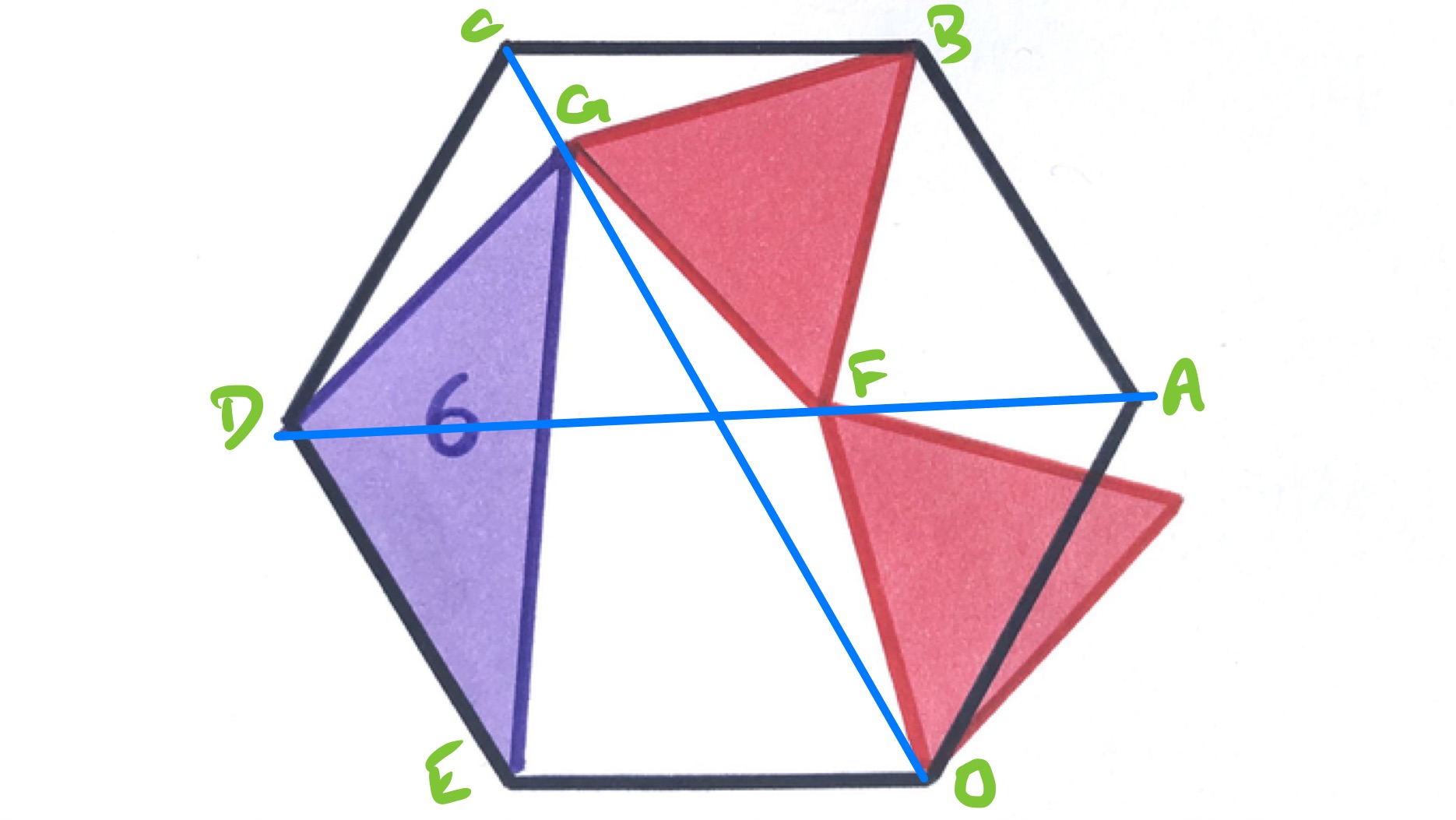
As the two equilateral triangles are the same size, the point in the above diagram is equidistant from and and so moves on the line that passes through and . Since can be obtained from by rotating it by clockwise about , it also moves on a straight line. To find the line, we consider two special cases of the diagram.
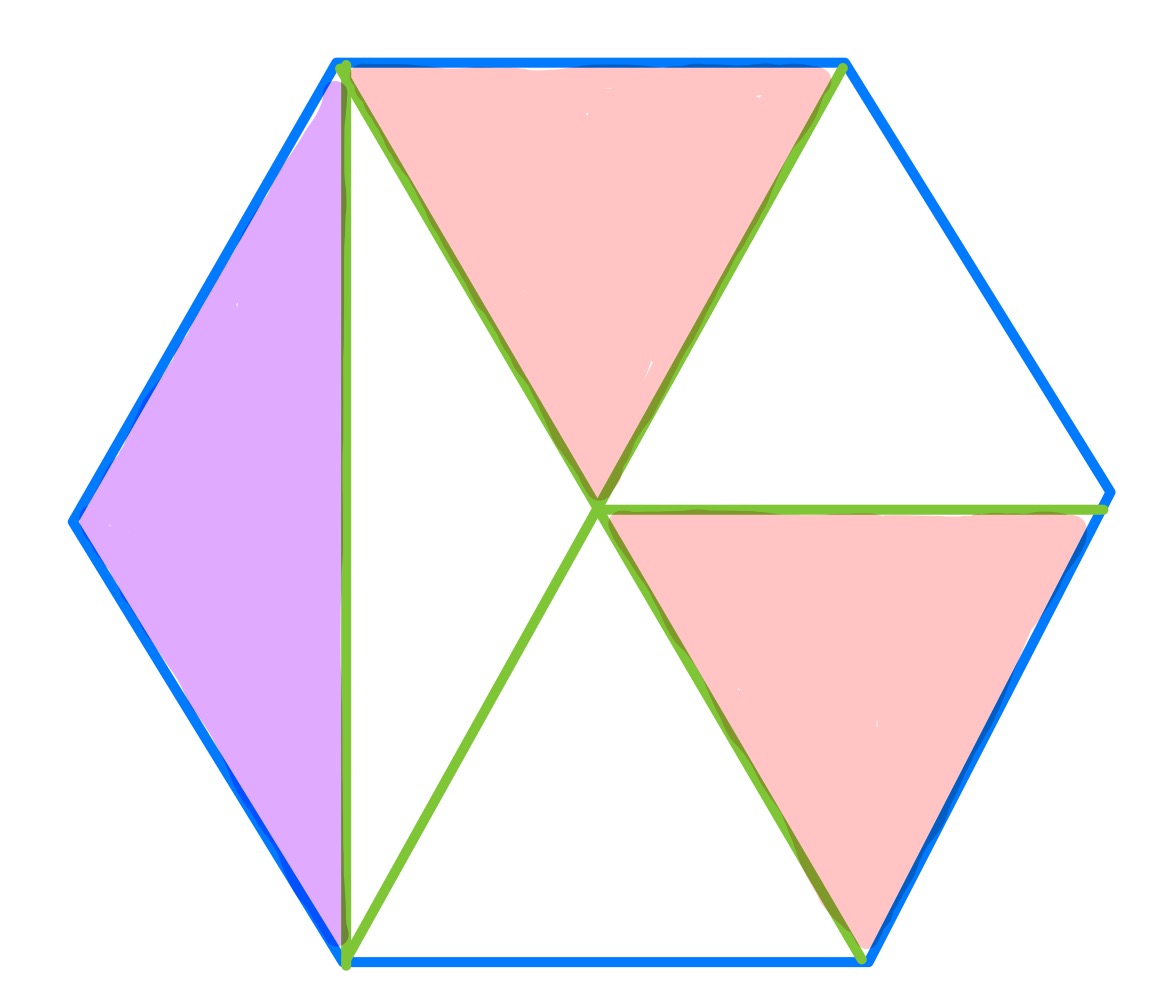
In this first special case, is at the centre of the hexagon and is coincident with .
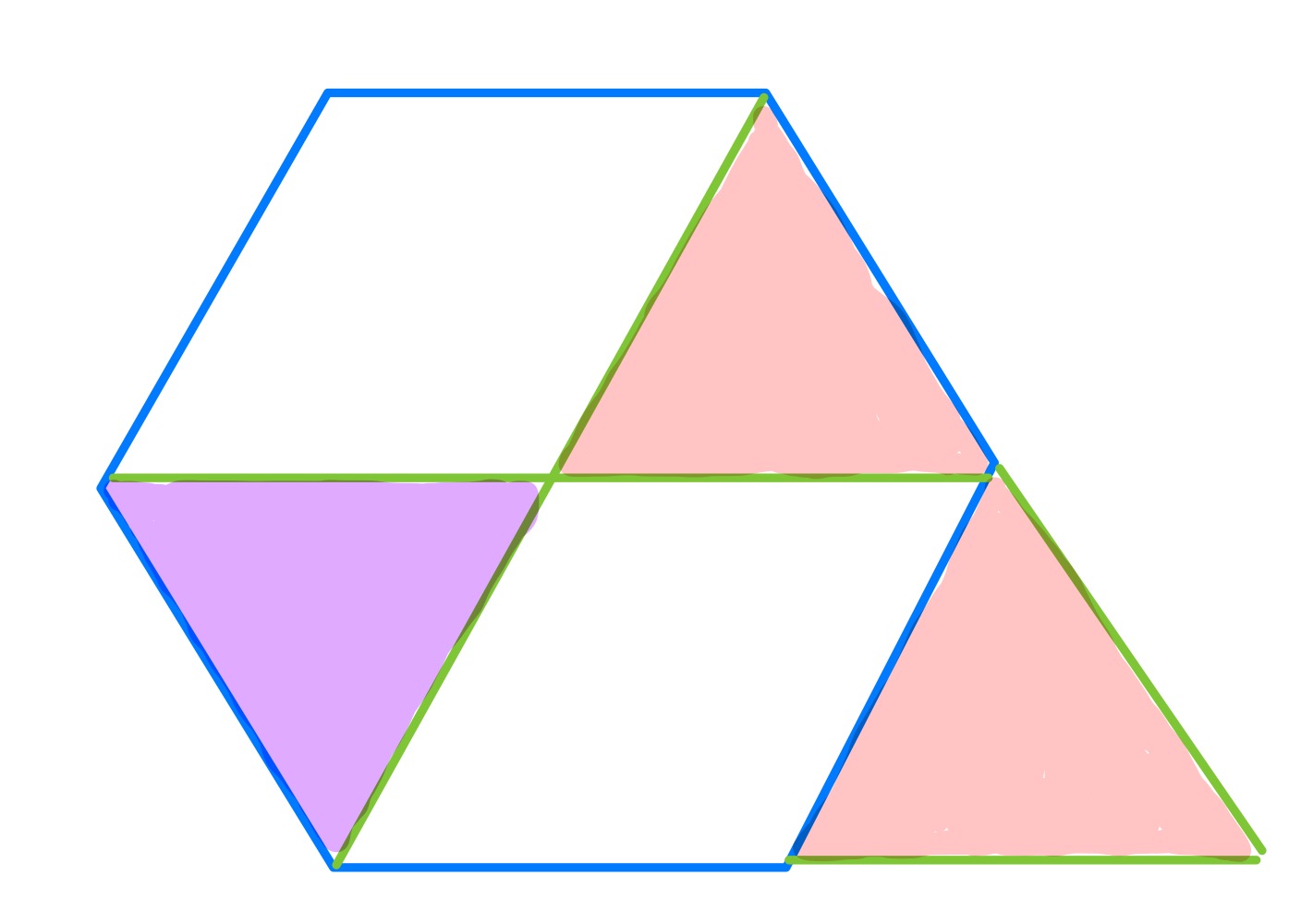
In the second special case, is coincident with and is at the centre of the hexagon.
The line that moves along is therefore the diagonal from to . This line is parallel to the side and so the “height” of the triangle above its “base” of is constant, relative to the length of . This means that the area of the triangle is a fixed fraction of the area of the hexagon. By considering the second special case it is clear that the triangle is th of the hexagon and so the hexagon has area .
Solution by Invariance Principle
Either of the special cases described above shows that the area of the purple triangle is one sixth of the area of the hexagon.