Notes
three triangles in a circle in a triangle solution
Solution to the Three Triangles in a Circle in a Triangle Puzzle
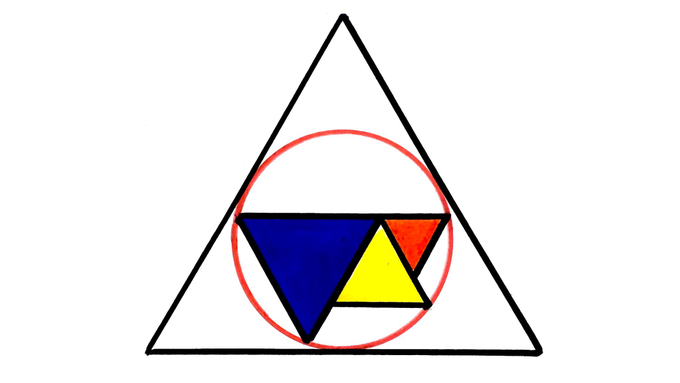
All four triangles are equilateral. What fraction of the largest triangle is shaded?
Solution by Angles in the Same Segment, the Cosine Rule, and the Intersecting Chords Theorem.
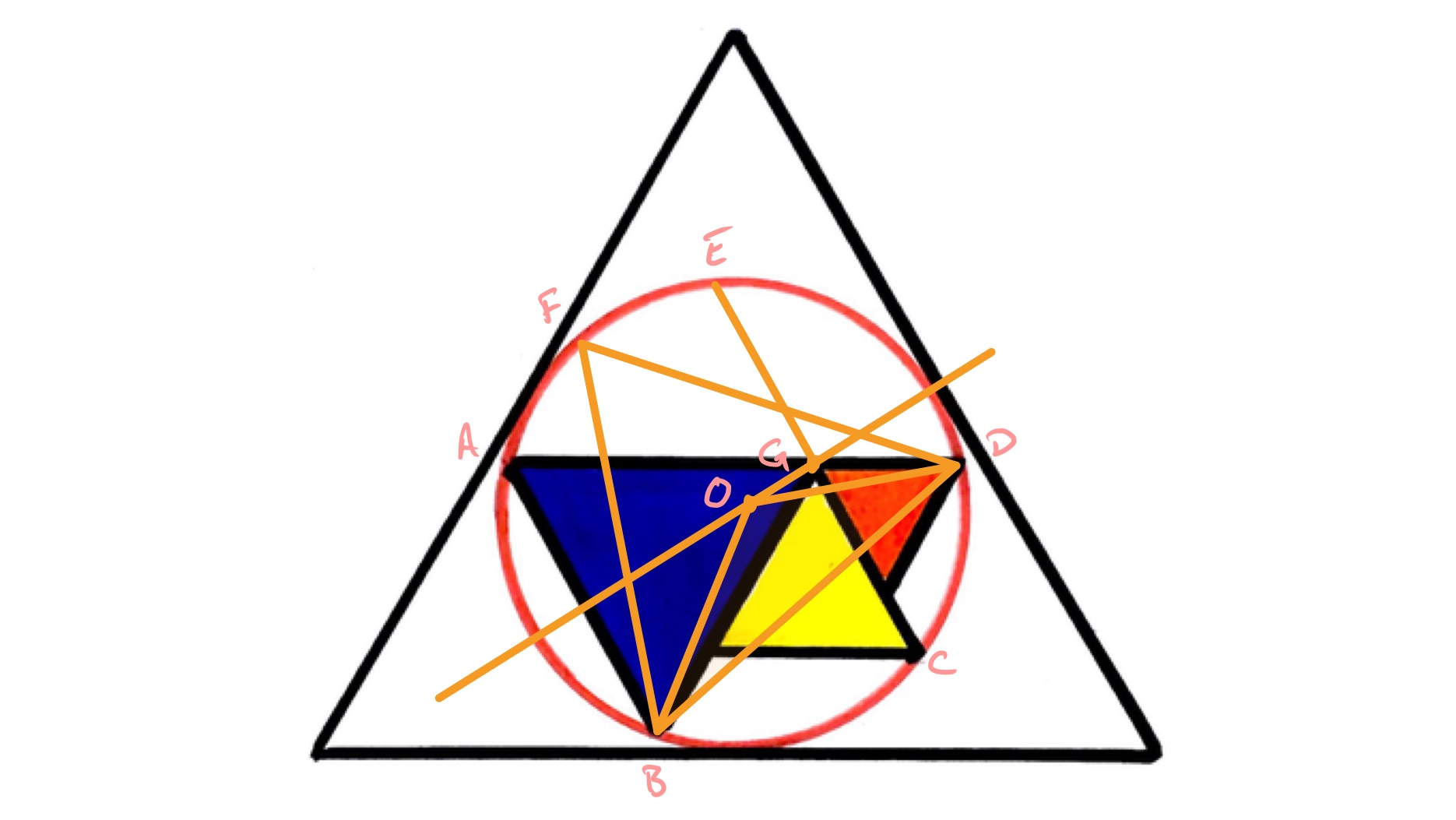
In the above diagram, the point is the centre of the circle, the point lies on the circumference so that triangle is isosceles, and is such that is a straight line.
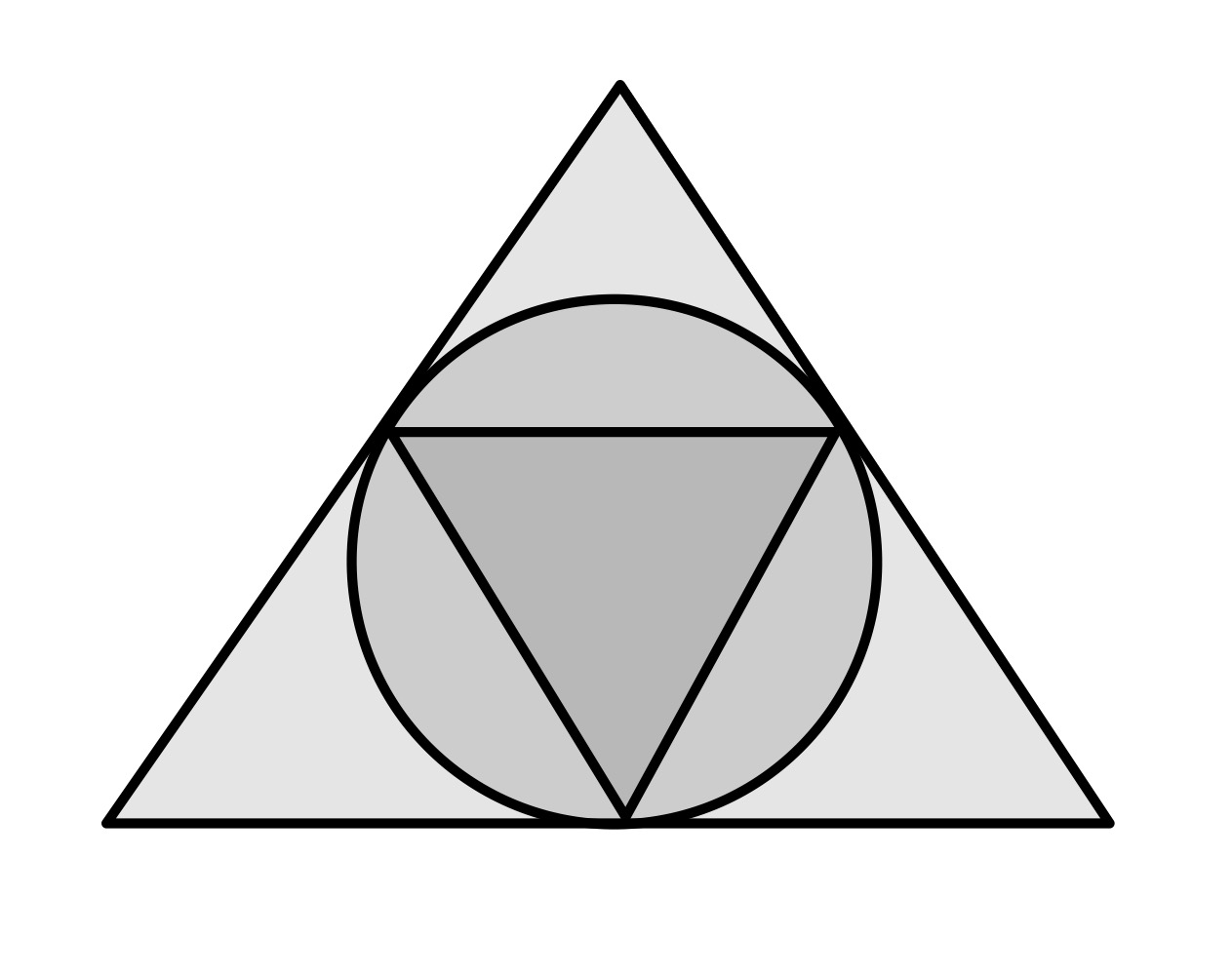
Since triangle is equilateral angle is and so, using the result that angles in the same segment are equal, angle is and so since triangle is, by construction, isosceles it is in fact equilateral. Its area is unaffected by rotating it, and it can be rotated to bring to where the circle touches one side of the outer equilateral triangle. This brings the configuration to the following diagram in which it is clear that the area of triangle is one quarter of the outer triangle.
Let be the length of , of , of , of . Angle is since both and are . Applying the cosine rule to triangle yields the identity:
Using , this simplifies to:
As is a chord of the circle, the perpendicular bisector of passes through . Since triangle is equilateral, that bisector also passes through and is a line of symmetry of triangle . Angle is therefore and so under reflection through the line extending the point is taken to meaning that the length of is the same as that of , namely .
Applying the intersecting chords theorem to the chords and then shows that . Putting this in the above equation gives:
Multiplying through by shows that the areas of the three shaded triangles is the same as that of triangle and hence is a quarter of the area of the outer triangle.