Notes
three tilted rectangles solution
Solution to the Three Tilted Rectangles Puzzle
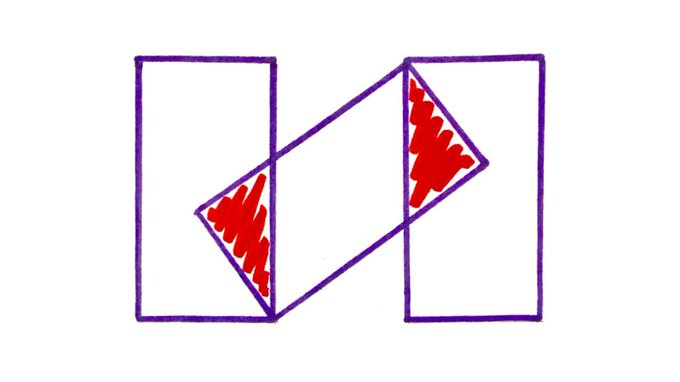
This design is made of three rectangles. What fraction of it is shaded?
Solution by Symmetry and Pythagoras' Theorem
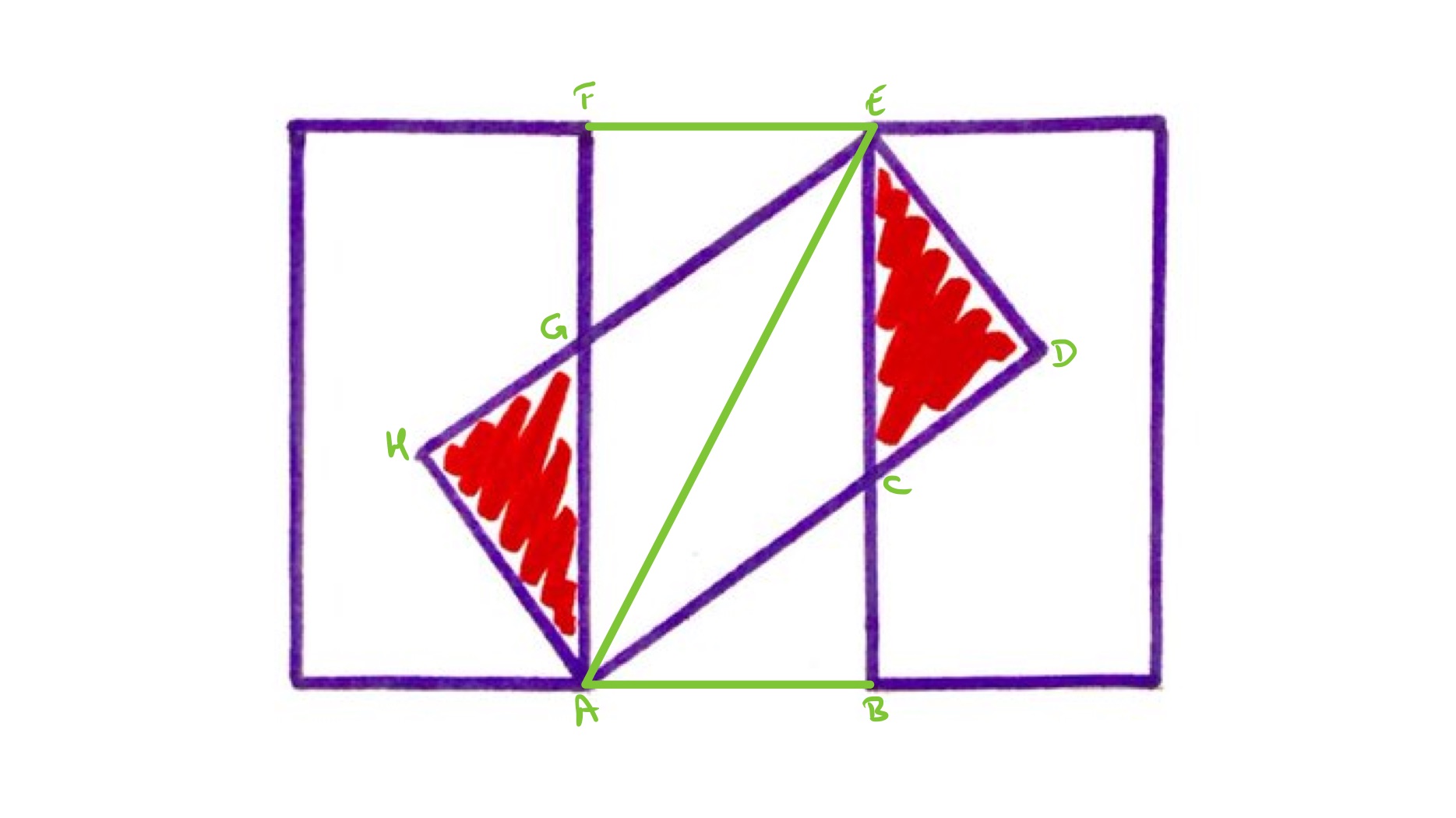
With the points labelled as above, the line is a diagonal of the tilted rectangle and reflecting the tilted rectangle in this line results in the rectangle , showing that is the same length as .
Let be the length of , so then has length . Let be the length of . Then has length since and are the same length. Applying Pythagoras' theorem to triangle shows that:
which rearranges to so . The shaded region therefore has area .
The area of the total design is equivalent to three rectangles of area each with the red regions removed, so the total area is .
The shaded region is therefore th of the total design.