Notes
three stacked squares solution
Solution to the Three Stacked Squares Puzzle
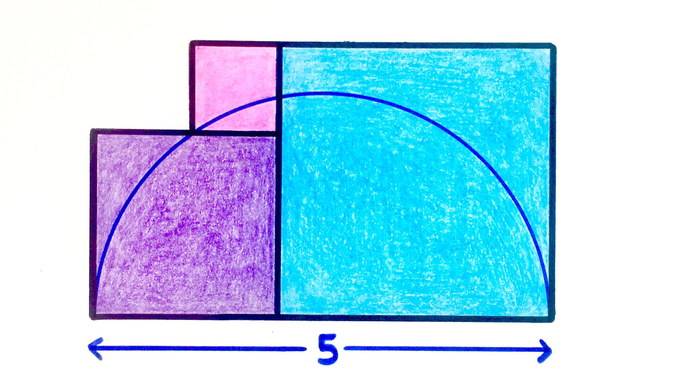
What’s the total area of these three squares?
Solution by Pythagoras' Theorem
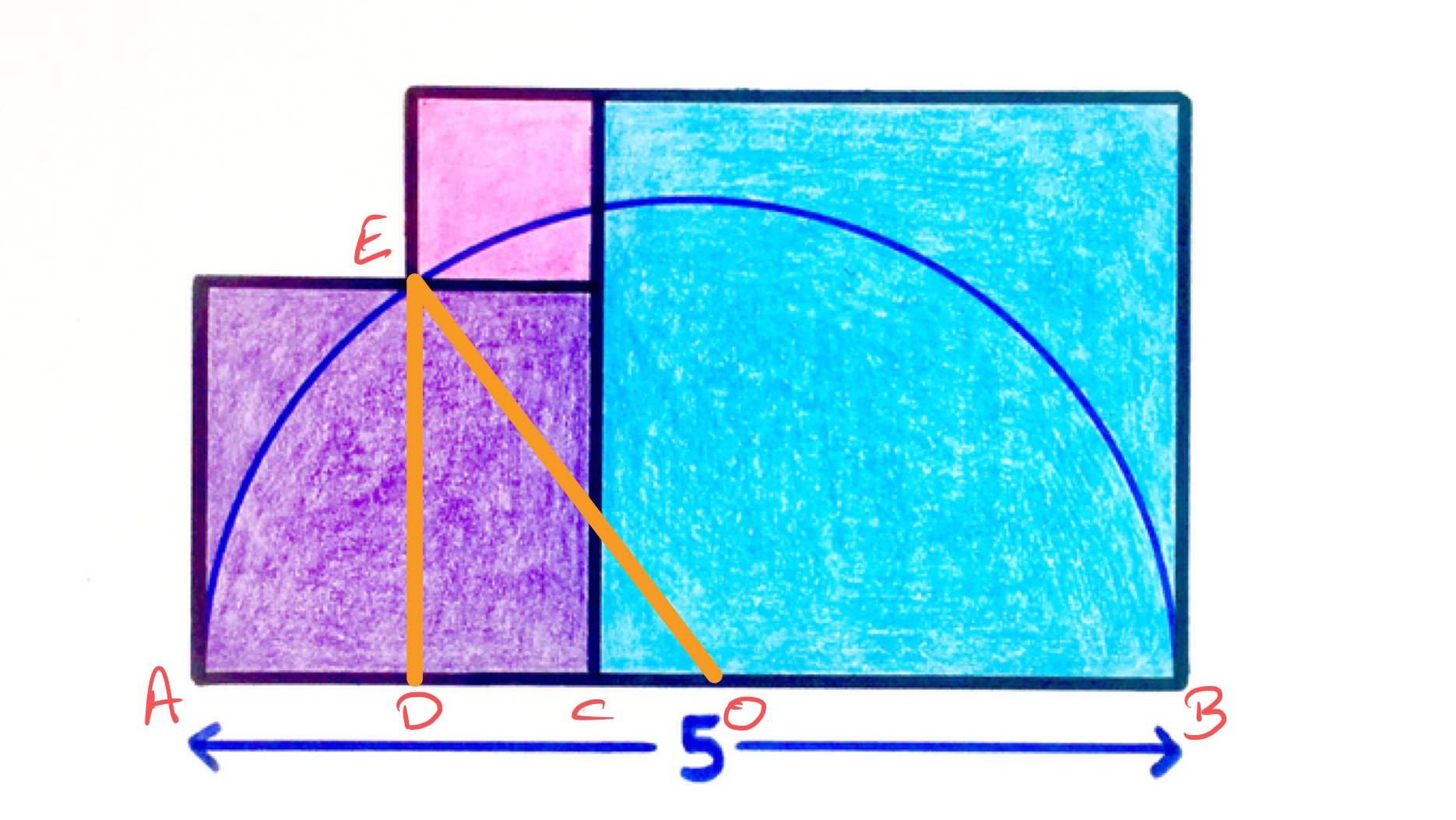
Let , , be the side lengths of the three squares in increasing order. Since the smaller squares stack against the larger, . Since the two larger squares stretch across the semi-circle, . So and .
With the points labelled as in the diagram, is a radius of the semi-circle so has length , has length , and has length . The length of is the length of minus the radius, so is .
Pythagoras' theorem applies to triangle , meaning that
This simplifies to which factors as so or . But if then and so there wouldn’t be three squares.
With , then and , so the total area is .